Invariants of projective space III: Motives
Monday, December 10th, 2012 | Author: Konrad Voelkel
I want to explain a particularly easy example of a motivic cellular decomposition: That of  -dimensional projective space. The discussion started with cohomology (part 1), continued with bundles and cycles (part 2) and in this part 3, we discuss motivic stuff.
-dimensional projective space. The discussion started with cohomology (part 1), continued with bundles and cycles (part 2) and in this part 3, we discuss motivic stuff.
Motives
Chow motive of projective space
One can compute the Chow motive of projective space by guessing it and using Manin's identity principle, a variant of the Yoneda lemma. To do such a "calculation" in general, the guessing part will be a problem. We can try to do systematic guessing. In fact, the previous two posts on projective space have prepared this. We expect, from the Weil cohomology computations, to have a motive ![h(\mathbb{P}^n) = \bigoplus_{s=0}^n 1(-s)[-2s]](https://www.konradvoelkel.com/wp-content/plugins/latex/cache/tex_bc5971942a706f2d2711f3f2f0c157e0.gif) (we can forget about the grading and the
(we can forget about the grading and the ![[-2s]](https://www.konradvoelkel.com/wp-content/plugins/latex/cache/tex_5898ab3ee52e4822f620adad97ebff40.gif) for now).
for now).
Manin's identity principle states that the functor that maps a motive 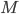 to the functor
to the functor

is fully faithful (where the grading on the right hand side is taken to be the grading in intersection groups). If you know the Yoneda lemma, this is an easy consequence. If you don't know the Yoneda lemma, you should be sitting at your desk, trying to prove it!
We compare the motives  and
and  by looking at their corresponding functors
by looking at their corresponding functors  . The only input we need from intersection theory is a projective bundle formula
. The only input we need from intersection theory is a projective bundle formula
![A^\bullet(X \times \mathbb{P}^n) \simeq A^\bullet(X)_F[H]/(H^{n+1}) = \bigoplus_{s=0}^n A^\bullet(X) \cdot H^s.](https://www.konradvoelkel.com/wp-content/plugins/latex/cache/tex_a2f91ef6f7941458ebff257e63793c22.gif)
We compute for any  :
:
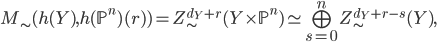

Using the first line with  and
and  we can take the identity on
we can take the identity on  to yield a canonical morphism
to yield a canonical morphism  , which is an isomorphism, since it induces an isomorphism of corresponding functors.
, which is an isomorphism, since it induces an isomorphism of corresponding functors.
We can use this now to compute realizations of the Chow motive. As we have seen, we just need to know how the Lefschetz motive ![1(-1)[-2]](https://www.konradvoelkel.com/wp-content/plugins/latex/cache/tex_93208923b7bddfe9abe2f8e256b2cb60.gif) realizes, i.e. what a Weil cohomology does on
realizes, i.e. what a Weil cohomology does on 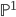 . For example, Betti realization
. For example, Betti realization  gives us a one-dimensional vector space
gives us a one-dimensional vector space  with Hodge decomposition
with Hodge decomposition  . The
. The  -adic realization gives us a one-dimensional vector space
-adic realization gives us a one-dimensional vector space  , where
, where  is the
is the 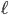 -adic Tate module of roots of unity
-adic Tate module of roots of unity 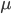 , which has a natural Galois action (which is part of the realization). Consequently,
, which has a natural Galois action (which is part of the realization). Consequently,  with Hodge decomposition
with Hodge decomposition  and
and  .
.
We could have skipped the Weil cohomology computations for  , it would have sufficed to compute the motive and the realizations of
, it would have sufficed to compute the motive and the realizations of 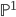 . But how would we have guessed the motive then? Well, using geometry. I will come to that later in this article.
. But how would we have guessed the motive then? Well, using geometry. I will come to that later in this article.
Voevodsky motives
Now I want to describe the motive of projective space (and its decomposition) in Voevodsky's framework of the derived category of mixed motives (which isn't constructed as the derived category of an abelian category, however it looks like that). By a general theorem (which is not too hard), the motive of a smooth projective variety is in the image of a (contravariant!) functor from Chow motives, so we don't need to work any longer for projective space. The following is for educational purposes only. I want to consider only perfect fields  , since I don't know what's possible for non-perfect fields.
, since I don't know what's possible for non-perfect fields.
The triangulated category of effective geometrical motives over  , denoted
, denoted  is defined as the pseudo-abelian envelope of a localization (at the minimal thick subcategory containing
is defined as the pseudo-abelian envelope of a localization (at the minimal thick subcategory containing  and Mayer-Vietoris sequences) of the homotopy category of bounded complexes over
and Mayer-Vietoris sequences) of the homotopy category of bounded complexes over  , the category of finite correspondences of smooth schemes over
, the category of finite correspondences of smooth schemes over  . We denote the image of a smooth scheme
. We denote the image of a smooth scheme  in this category by
in this category by  (following Voevodsky).
(following Voevodsky).
A few easy calculations:
Since we have the pseudo-abelian property, we can do at least the usual splitting  , where
, where  is the unit object for the tensor structure and
is the unit object for the tensor structure and  is the reduced motive of
is the reduced motive of 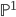 . The Tate object is defined as
. The Tate object is defined as ![\mathbb{Z}(1) := \mathbb{L}[-2]](https://www.konradvoelkel.com/wp-content/plugins/latex/cache/tex_718a21635908fac0057444c7ff1aef28.gif) (warning: Voevodsky motives are covariant, while Chow motives are contravariant, hence some formula look different; this is such a formula).
(warning: Voevodsky motives are covariant, while Chow motives are contravariant, hence some formula look different; this is such a formula).
For Mayer-Vietoris, we can take the usual two charts  which are a Zariski open covering of
which are a Zariski open covering of  , so there is a distinguished triangle
, so there is a distinguished triangle
![M_{gm}(U\cap V) \to M_{gm}(U) \oplus M_{gm}(V) \to M_{gm}(X) \to M_{gm}(U \cap V)[1]](https://www.konradvoelkel.com/wp-content/plugins/latex/cache/tex_f91224aa01c5c619d9901701d5b63a07.gif)
which in our case looks like
![M_{gm}(\mathbb{G}_m) \to 0 \oplus 0 \to M_{gm}(\mathbb{P}^1) \to M_{gm}(\mathbb{G}_m)[1]](https://www.konradvoelkel.com/wp-content/plugins/latex/cache/tex_c3b75885970f3ba8607808471d79ee0c.gif)
so that ![M_{gm}(\mathbb{P}^1) \to M_{gm}(\mathbb{G}_m)[1]](https://www.konradvoelkel.com/wp-content/plugins/latex/cache/tex_57a57595aec0ae0ce5786f628e9a9396.gif) is an isomorphism.
is an isomorphism.
To work with these motives, it is better to look at another category, which is denoted by  . A presheaf with transfers on
. A presheaf with transfers on  is an additive contravariant functor from
is an additive contravariant functor from  to abelian groups. Such a presheaf with transfers can be seen as a presheaf on
to abelian groups. Such a presheaf with transfers can be seen as a presheaf on  with additional restriction maps for each correspondence which isn't the graph of a morphism; in particular for the transposed graphs, which give restriction maps "in the other direction", hence the name "with transfers". A presheaf with transfers on
with additional restriction maps for each correspondence which isn't the graph of a morphism; in particular for the transposed graphs, which give restriction maps "in the other direction", hence the name "with transfers". A presheaf with transfers on  is called Nisnevich sheaf if the corresponding presheaf of abelian groups on
is called Nisnevich sheaf if the corresponding presheaf of abelian groups on  is a Nisnevich sheaf. A (pre)sheaf with transfers is called homotopy invariant if every projection map
is a Nisnevich sheaf. A (pre)sheaf with transfers is called homotopy invariant if every projection map  induces an isomorphism of sections. Now
induces an isomorphism of sections. Now  is the full subcategory of
is the full subcategory of  of complexes with homotopy invariant cohomology sheaves. This category is a triangulated pseudo-abelian category. One can show that
of complexes with homotopy invariant cohomology sheaves. This category is a triangulated pseudo-abelian category. One can show that  admits a full embedding (as tensor triangulated category) into
admits a full embedding (as tensor triangulated category) into  .
.
Both categories of effective motives yield larger categories of motives by inverting the Tate twist operation  , thus one has
, thus one has  a full tensor triangulated subcategory of
a full tensor triangulated subcategory of  . Now one could write down a Gysin sequence and a projective bundle theorem which can be used to compute the motive of
. Now one could write down a Gysin sequence and a projective bundle theorem which can be used to compute the motive of  , entirely in terms of
, entirely in terms of  ; the problem is that the proof I know of goes through the computation of the motive of
; the problem is that the proof I know of goes through the computation of the motive of  , in terms of
, in terms of  .
.
Denote by 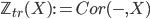 the presheaf with transfers associated to a smooth scheme
the presheaf with transfers associated to a smooth scheme  and by
and by  the complex obtained from the simplicial object
the complex obtained from the simplicial object  .
.
Voevodsky motive of projective space
We use ![\mathbb{Z}(q) := C_\ast\mathbb{Z}_{tr}(\mathbb{G}_m^{\wedge q})[-q]](https://www.konradvoelkel.com/wp-content/plugins/latex/cache/tex_7751a2f75c8fd5bd26cf6feed01cd8be.gif) , which is called a motivic complex. We have already discussed
, which is called a motivic complex. We have already discussed ![M_{gm}(\mathbb{P}^1) = M_{gm}(\mathbb{G}_m)[1]](https://www.konradvoelkel.com/wp-content/plugins/latex/cache/tex_13056afe85bd8ac1028e53d3eec083f9.gif) . In a similar spirit, we have
. In a similar spirit, we have ![C_\ast\mathbb{Z}_{tr}(\mathbb{P}^1) = \mathbb{Z}(1)[2]](https://www.konradvoelkel.com/wp-content/plugins/latex/cache/tex_e11f916c1e98e37e59c2fa2051d22ba7.gif) , using the following lemma: for
, using the following lemma: for  a Zariski covering of
a Zariski covering of  the Cech resolution
the Cech resolution  is a quasi-isomorphism in the Zariski topology.
is a quasi-isomorphism in the Zariski topology.
Let's denote ![0 := [1:0:\cdots:0] \in \mathbb{P}^n](https://www.konradvoelkel.com/wp-content/plugins/latex/cache/tex_b7b2c4c1f575419b51dec5bafdf4668f.gif) and look at the map
and look at the map  given by
given by ![[x_0:\cdots:x_n] \mapsto [x_1:\cdots:x_n]](https://www.konradvoelkel.com/wp-content/plugins/latex/cache/tex_fc1f38dcfea971f89739f4d5b962b826.gif) . The fibers of this map are just
. The fibers of this map are just  . There is an
. There is an  -homotopy inverse
-homotopy inverse 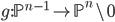 given by the section
given by the section ![[x_1:\cdots:x_n] \mapsto [0:x_1:\cdots:x_n]](https://www.konradvoelkel.com/wp-content/plugins/latex/cache/tex_8de4033aa466939fc50acc96ae12629c.gif) , and the
, and the  -homotopy of
-homotopy of  to
to  is given by multiplication of
is given by multiplication of  with
with  . Such a pair of
. Such a pair of  -homotopy inverse maps yield a chain homotopy equivalence
-homotopy inverse maps yield a chain homotopy equivalence 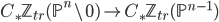 .
.
Theorem: For each  , there are quasi-isomorphisms of Zariski sheaves:
, there are quasi-isomorphisms of Zariski sheaves:
![C_\ast\left( \mathbb{Z}_{tr}(\mathbb{P}^n)/\mathbb{Z}_{tr}(\mathbb{P}^{n-1}) \right) \simeq C_\ast \mathbb{Z}_{tr}(\mathbb{G}_m^{\wedge n})[n] = \mathbb{Z}(n)[2n]](https://www.konradvoelkel.com/wp-content/plugins/latex/cache/tex_0cd6cbd13871bfe9d8ee0482da811f8f.gif) .
.
The proof of this theorem (which I got from the Mazza-Voevodsky-Weibel book, Chapter 15) uses a few facts about presheaves with transfers, for example the Nisnevich sheafification  of a homotopy invariant presheaf with transfers
of a homotopy invariant presheaf with transfers  is again homotopy invariant; and more is true: all the presheaves
is again homotopy invariant; and more is true: all the presheaves 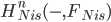 are homotopy invariant. Using this, one can show that a presheaf with transfers
are homotopy invariant. Using this, one can show that a presheaf with transfers  that satisfies
that satisfies 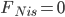 also satisfies
also satisfies  and
and  .
.
Proof sketch: Let  be the usual cover of
be the usual cover of  by
by  charts
charts 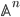 and let
and let  be the cover by
be the cover by  charts of
charts of  . Intersecting
. Intersecting  charts gives
charts gives 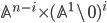 . There are quasi-isomorphisms (of complexes of Nisnevich sheaves with transfers)
. There are quasi-isomorphisms (of complexes of Nisnevich sheaves with transfers)  and
and  , so
, so  is a resolution of
is a resolution of  (as Nisnevich sheaf). Now
(as Nisnevich sheaf). Now  is quasi-isomorphic to
is quasi-isomorphic to 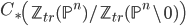 , hence to
, hence to  for the Zariski topology.
for the Zariski topology.
One can write down a resolution  of
of ![\mathbb{Z}_{tr}(\mathbb{G}_m^{\wedge n})[n]](https://www.konradvoelkel.com/wp-content/plugins/latex/cache/tex_fd5c38219171003abfd759d2f7e9e26f.gif) such that one gets a map
such that one gets a map  whose terms are direct sums of
whose terms are direct sums of  -homotopy equivalences, so
-homotopy equivalences, so  is a quasi-isomorphism. Applying
is a quasi-isomorphism. Applying  gives us
gives us
![C_\ast\left(\mathbb{Z}_{tr}(\mathbb{P}^n)/\mathbb{Z}_{tr}(\mathbb{P}^{n-1})\right) \simeq Tot C_\ast Q_\ast \simeq Tot C_\ast R_\ast \simeq C_\ast \mathbb{Z}_{tr}(\mathbb{G}_m^{\wedge n})[n]](https://www.konradvoelkel.com/wp-content/plugins/latex/cache/tex_ba5e82f5f11d7470b185669c29969b9b.gif) .
.
One can show that the isomorphism in this theorem factors through every inclusion 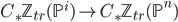 with
with 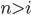 .
.
Corollary: There is a quasi-isomorphism ![M(\mathbb{P}^n)=C_\ast\mathbb{Z}_{tr}(\mathbb{P}^n) \to \bigoplus_{s=0}^n \mathbb{Z}(s)[2s]](https://www.konradvoelkel.com/wp-content/plugins/latex/cache/tex_7152cce51ca5f0c99d6ae4f45899d35b.gif) .
.
Proof: by induction, where the case 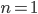 is already done. The map
is already done. The map  is split injective in
is split injective in  , since the quasi-isomorphism
, since the quasi-isomorphism ![\mathbb{Z}_{tr}(\mathbb{P}^{n-1}) \to \bigoplus_{s=0}^{n-1} \mathbb{Z}(s)[2s]](https://www.konradvoelkel.com/wp-content/plugins/latex/cache/tex_04e721f7758f3705e6976cab0a185b40.gif) (from the induction hypothesis) factors through it. Hence the distinguished triangle
(from the induction hypothesis) factors through it. Hence the distinguished triangle
![C_\ast \mathbb{Z}_{tr}(\mathbb{P}^{n-1}) \to C_\ast \mathbb{Z}_{tr}(\mathbb{P}^{n}) \to \mathbb{Z}(n)[n] \to [1]](https://www.konradvoelkel.com/wp-content/plugins/latex/cache/tex_84d58be48c07f77d6ee663f696cec710.gif)
splits.
Computations from the motive: motivic cohomology
Now that we have the motive, we can (in principle) compute motivic cohomology

where the Ext is in the category of Nisnevich sheaves with transfer.
So we have to understand ![Hom_{DM_{-}}(\mathbb{Z}(s)[2s],\mathbb{Z}(q)[p])](https://www.konradvoelkel.com/wp-content/plugins/latex/cache/tex_9782615e3623ee3d25805d5b47465625.gif) . This can be simplified to
. This can be simplified to ![Hom(\mathbb{Z},\mathbb{Z}(q-s)[p-2s]) = H^{p-2s,q-s}_{mot}(Spec(k))](https://www.konradvoelkel.com/wp-content/plugins/latex/cache/tex_2bb0dd41bfef63f2ab00e7e40c89edcf.gif) , so we are reduced to understand the motivic cohomology of a point.
, so we are reduced to understand the motivic cohomology of a point.
From the motivic cycle class isomorphism 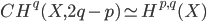 one can recover the Chow groups of
one can recover the Chow groups of  . The motivic Chern character yields an isomorphism computing the algebraic K-Theory of
. The motivic Chern character yields an isomorphism computing the algebraic K-Theory of  (see this article about the divisorial jungle, where I discuss this briefly).
(see this article about the divisorial jungle, where I discuss this briefly).
A¹-homotopy type and motivic cell structure
We can take one step backwards and look at  not with (co)homological eyes, but with homotopical ones. The functor
not with (co)homological eyes, but with homotopical ones. The functor  factors through a model category
factors through a model category  of simplicial Nisnevich sheaves on
of simplicial Nisnevich sheaves on  , where one can do homotopy theory.
, where one can do homotopy theory.
In this model category  one can write down
one can write down  , a space (=simplicial Nisnevich sheaf) which has the same motive as
, a space (=simplicial Nisnevich sheaf) which has the same motive as  , since wedging with the
, since wedging with the  -dimensional simplicial sphere
-dimensional simplicial sphere  induces a shift by
induces a shift by  , hence
, hence ![M(\mathbb{G}_m^{\wedge s} \wedge S^s_s) = \mathbb{Z}(s)[2s]](https://www.konradvoelkel.com/wp-content/plugins/latex/cache/tex_71121573fe7ea4acd30f2401b9ba1da3.gif) . One could now try to write down (or prove existence of) an
. One could now try to write down (or prove existence of) an  -homotopy equivalence of
-homotopy equivalence of  with
with  .
.
This turns out to be impossible in general, since the homotopy types are different (but they become isomorphic over a quadratically closed base field). We can already see that in the real realization, which is a functor that assigns to a homotopy type a topological space which acts like the 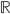 -points. The projective space has non-orientable real realization, while
-points. The projective space has non-orientable real realization, while  is orientable. This is like the difference between
is orientable. This is like the difference between  and
and  .
.
One can write down a motivic cell structure for  , where the attaching maps split over a quadratically closed field. One can say that motives don't distinguish between
, where the attaching maps split over a quadratically closed field. One can say that motives don't distinguish between  and
and  , but the homotopy type does (even the stable homotopy type).
, but the homotopy type does (even the stable homotopy type).
Such a motivic cell structure can be constructed like in topology: start with a point  and attach a 1-cell
and attach a 1-cell  along the attaching map
along the attaching map  which is the quotient map after the
which is the quotient map after the  -action. You get a
-action. You get a 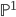 . Then attach a 2-cell
. Then attach a 2-cell  along
along  , you get
, you get  and so on.
and so on.
We get the motive out of a motivic cell structure, since a cofiber sequence 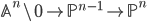 yields a distinguished triangle and
yields a distinguished triangle and  has the motive
has the motive ![\mathbb{Z}(n)[2n-1]](https://www.konradvoelkel.com/wp-content/plugins/latex/cache/tex_02e91771d143b90c094d68985ad01f54.gif) , so we can write the distinguished triangle as
, so we can write the distinguished triangle as
![M(\mathbb{P}^{n-1}) \to M(\mathbb{P}^n) \to \mathbb{Z}(n)[2n] \to](https://www.konradvoelkel.com/wp-content/plugins/latex/cache/tex_3c712a559ebb49e46c1c6977a8970dee.gif)
which splits, i.e. ![M(\mathbb{P}^n) = M(\mathbb{P}^{n-1}) \oplus \mathbb{Z}(n)[2n]](https://www.konradvoelkel.com/wp-content/plugins/latex/cache/tex_64edc621290ef4d88fa8b99aaa901dc8.gif) , since the morphism
, since the morphism ![\mathbb{Z}(n)[2n-1] \to M(\mathbb{P}^{n-1})](https://www.konradvoelkel.com/wp-content/plugins/latex/cache/tex_9a929c3762af0d1dfd920195175e3a79.gif) is trivial.
is trivial.
This is the calculation of the motive, thus of higher Chow groups, algebraic K-Theory and all Weil cohomology theories, that I like most.
