Cellular objects in the motivic model category
Friday, November 16th, 2012 | Author: Konrad Voelkel
This article explains the notion of cellular objects in the motivic model category, which are like CW complexes for the algebraic/motivic world.
(last edit on 2014-04-08, added a remark on realizations and a Thom construction)
Cellular objects in a model category
Definition: Fix a set  of objects in a model category
of objects in a model category  , then an
, then an  -cellular object in
-cellular object in  is an object obtained by iterative homotopy colimits of objects in
is an object obtained by iterative homotopy colimits of objects in  . More precisely, the class of
. More precisely, the class of  -cellular objects is the smallest class of objects that contains
-cellular objects is the smallest class of objects that contains  and is closed under weak equivalence and homotopy colimits.
and is closed under weak equivalence and homotopy colimits.
Example:  the class of spheres
the class of spheres  in the model category
in the model category  of topological spaces (with Hurewicz fibrations and weak homotopy equivalences), then
of topological spaces (with Hurewicz fibrations and weak homotopy equivalences), then  -cellular objects are CW-complexes.
-cellular objects are CW-complexes.
Warning: with this definition, every topological space is a CW complex. This comes from the fact that homotopy colimits are only defined up to weak equivalence and CW approximation gives you a weakly equivalent CW complex for every topological space. However, it doesn't give you a cell structure (the data of the gluing maps), which is what we really care about.
Cell structures in algebraic geometry
There are many places in algebraic geometry where one encounters things like "cell structures". Sometimes this means there is a stratification with strata being affine spaces, or something similar. The main difference between these, colloquially called cellular varieties, and honest cellular varieties in the spirit of the previous definition, is the absence of attaching maps, which describe how to glue the cells together.
Sadly, in many cases where people talk about "cellular varieties" the corresponding attaching maps don't exist, or/and the obvious choice turns out to be non-algebraic. This doesn't mean that naive cellularity is a bad notion, it just means that honest cellularity (in our sense) is a stronger notion.
In A¹-homotopy theory
The spheres one has in algebraic homotopy theory are manifold (sorry, I love these jokes):
- Projective line

- Multiplicative group

- Affine space without origin
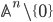
- The simplicial presheaf which is constant the simplicial sphere

- The "Thom space"

In motivic homotopy theory one can reduce these to two sources: 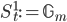 , called the Tate sphere, and
, called the Tate sphere, and  , called simplicial sphere. Together they give us products
, called simplicial sphere. Together they give us products  called motivic spheres.
called motivic spheres.
The class  consisting of all motivic spheres, in the model category of Morel-Voevodsky on simplicial (pre)sheaves on the Nisnevich site of smooth projective schemes over a field, yield the notion of motivic cellularity.
consisting of all motivic spheres, in the model category of Morel-Voevodsky on simplicial (pre)sheaves on the Nisnevich site of smooth projective schemes over a field, yield the notion of motivic cellularity.
The other sphere candidates also have their place in this theory, since 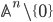 , after choosing a basepoint, has the weak homotopy type of
, after choosing a basepoint, has the weak homotopy type of  and
and  is weakly equivalent to
is weakly equivalent to  . In this new notation we also have now
. In this new notation we also have now 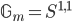 and
and  . One can also show
. One can also show  .
.
There is the real and the complex realization. In both, simplicial things realize to their geometric realization. The complex realization of a variety just takes the analytification of the complex points, where the real realization then proceeds by taking Galois fixed points. Hence the complex realization of  is
is  and consequently
and consequently 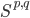 realizes to
realizes to 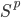 . On the other hand, real realization of
. On the other hand, real realization of  is
is  , which is the unit for the smash product
, which is the unit for the smash product  , so the real realization of
, so the real realization of 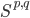 is
is  .
.
To summarize, a motivic cellular space is just a scheme such that there is a motivic cell structure, which means there are attaching maps from motivic spheres 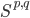 that build up the scheme. Of course, these maps are maps of simplicial presheaves, maybe not morphisms of schemes.
that build up the scheme. Of course, these maps are maps of simplicial presheaves, maybe not morphisms of schemes.
What is that good for? Well, as for CW complexes, a motivic cell structure immediately gives you the cohomology, in particular the motive. Each motivic cell (sphere) 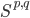 has a motive
has a motive ![M(S^{p,q}) = \mathbb{Z}(q)[p]](http://www.konradvoelkel.com/wp-content/plugins/latex/cache/tex_f577ceea78cc8e7837dd555ec3b593b5.gif) (since the motive of a wedge is a tensor product and we have
(since the motive of a wedge is a tensor product and we have ![M(\mathbb{G}_m)=\mathbb{Z}(1)[1]](http://www.konradvoelkel.com/wp-content/plugins/latex/cache/tex_6d14b1dddaf837be2e472b9451d91315.gif) as well as
as well as ![M(\Delta^n / \partial \Delta^n)=\mathbb{Z}[n]](http://www.konradvoelkel.com/wp-content/plugins/latex/cache/tex_9be297bad7bcf7f558d39d8b71994df0.gif) ) and you get a motivic decomposition. The motivic cell structure is more than that: the attaching maps contain more information.
) and you get a motivic decomposition. The motivic cell structure is more than that: the attaching maps contain more information.
Note that, since the motive ![\mathbb{Z}(q)[p]](http://www.konradvoelkel.com/wp-content/plugins/latex/cache/tex_579d22388ec2ff94b039d0f6c4eef7e2.gif) is a Tate motive (by definition, a Tate motive is an iterated extension, shift, twist of
is a Tate motive (by definition, a Tate motive is an iterated extension, shift, twist of  ), varieties with motivic cell structure also have Tate motives. To motives-people, this immediately makes motivic cell structures something nice to have.
), varieties with motivic cell structure also have Tate motives. To motives-people, this immediately makes motivic cell structures something nice to have.
Example: Projective space has a very simple decomposition of the motive, and I can write down two distinct motivic homotopy types with this motive. One is projective space itself (with a motivic cell structure), the other (non-weakly-equivalent) is just a wedge of spheres (also called "bouquet", with an obvious motivic cell structure). These two are not weakly equivalent since the attaching map for the cells in projective space is the Hopf map  , which is not null-homotopic (with
, which is not null-homotopic (with  -coefficients this is still true, but not any longer with coefficients in a quadratically closed field).
-coefficients this is still true, but not any longer with coefficients in a quadratically closed field).
Further reading: Dugger & Isaksen: Motivic cell structures (2005), and Wendt: More examples of motivic cell structures (2010)
Some known decompositions of motives
The decomposition of the Chow motive of projective space is known for some time: ![M(\mathbb{P}^n) = \bigoplus_{i=0}^n \mathbb{Z}(i)[2i]](http://www.konradvoelkel.com/wp-content/plugins/latex/cache/tex_031f86ace93d5388eb1e861c2f82d628.gif) . It can be obtained from a motivic cell decomposition, as I already said. This motivic cell decomposition may be obtained by an action of the multiplicative group
. It can be obtained from a motivic cell decomposition, as I already said. This motivic cell decomposition may be obtained by an action of the multiplicative group  with isolated fixed points, that mimics the gradient flow of a Morse function for algebraic geometry (which is called the method of Bialynicki-Birula).
with isolated fixed points, that mimics the gradient flow of a Morse function for algebraic geometry (which is called the method of Bialynicki-Birula).
Another (apparently) well-know decomposition of motives is the Rost decomposition of smooth projective isotropic quadrics  over fields of uneven characteristic:
over fields of uneven characteristic: ![M(Q) = \mathbb{Z} \oplus M(Q')(1)[2n-2] \oplus \mathbb{Z}(n)[2n]](http://www.konradvoelkel.com/wp-content/plugins/latex/cache/tex_8b862a6c0acfdcccae9d0ff131b44534.gif) . This decomposition may also be obtained from a motivic cell decomposition, which itself comes from the method of Bialynicki-Birula.
. This decomposition may also be obtained from a motivic cell decomposition, which itself comes from the method of Bialynicki-Birula.
There is a similar story for a result of Karpenko, and this story may be read in Brosnan: On motivic decompositions arising from the method of Bialynicki-Birula.
