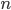In this post I'll do a few very explicit computations for motivic cell structures of smooth projective toric varieties coming from the Białynicki-Birula decomposition, namely $\mathbb{P}^1, \mathbb{P}^1 \times \mathbb{P}^1, \mathbb{P}^2$ and Hirzebruch surfaces. It is a bit lengthy but maybe helpful to anyone who wants to do some explicit calculations with BB-decompositions. I hope you're accustomed to toric varieties, but I won't do anything fancy. You can safely skip the motivic part of this post.

Continue reading «Motivic Cell Structure of Toric Surfaces»

This is about Białynicki-Birula's paper from '72 on actions of reductive linear algebraic groups on non-singular varieties, in particular Gm-operations on smooth projective varieties. I give a proof sketch of Theorem 4.1 therein and explain a little bit how Brosnan applied these results in 2005 to get decompositions of the Chow motive of smooth projective varieties with Gm-operation. Wendt used these methods in 2010 to lift such a decomposition on the homotopy-level, to prove that smooth projective spherical varieties admit stable motivic cell decompositions. Most of this blogpost consists of an outline of the B-B paper.

Continue reading «Białynicki-Birula and Motivic Decompositions»

I want to explain a particularly easy example of a motivic cellular decomposition: That of $n$-dimensional projective space. The discussion started with cohomology (part 1), continued with bundles and cycles (part 2) and in this part 3, we discuss motivic stuff.

Continue reading «Invariants of projective space III: Motives»

I want to explain a particularly easy example of a motivic cellular decomposition: That of $n$-dimensional projective space. The discussion started with cohomology (part 1) and in this part 2, we discuss intersection-theoretic and bundle-theoretic invariants. In part 3 we will see the motivic stuff.

Continue reading «Invariants of projective space II: Cycles and Bundles»

I want to explain a particularly easy example of a motivic cellular decomposition: That of $n$-dimensional projective space. We will have a look at the cohomology, the Chow groups and the algebraic K-theory of projective space -- a discussion probably interesting to non-motivic people as well. After these invariants, I will look at the motive and the A¹-homotopy type. Then I want to describe the decomposition of the motive (and the homotopy type) homotopy-theoretically, by means of cofiber sequences. (We will see that projective space is not isomorphic to a coproduct of motivic spheres with the same motive). Of course, nothing is new, I'm just working out exercises here.

In this part 1, I discuss only the cohomology of $\mathbb{P}^n$. Part 2 contains a discussion of the intersection theory and bundles and part 3 contains the motivic stuff. I intentionally left out usage of projective bundle formulas, as I will discuss them separately.

Continue reading «Invariants of projective space I: Cohomology»

This is a very short notice to memorize some of the various model structures on simplicial presheaves in a systematic way.

[UPDATE 2013-03-06] I gave a talk in our working group seminar about model structures on simplicial presheaves, homotopy sheaves and h-principles [/UPDATE]

Continue reading «Model structures on simplicial presheaves»