Invariants of projective space II: Cycles and Bundles
Thursday, December 06th, 2012 | Author: Konrad Voelkel
I want to explain a particularly easy example of a motivic cellular decomposition: That of  -dimensional projective space. The discussion started with cohomology (part 1) and in this part 2, we discuss intersection-theoretic and bundle-theoretic invariants. In part 3 we will see the motivic stuff.
-dimensional projective space. The discussion started with cohomology (part 1) and in this part 2, we discuss intersection-theoretic and bundle-theoretic invariants. In part 3 we will see the motivic stuff.
The invariants discussed in this article are closely related and I wrote an article about the divisorial jungle before.
Divisor class group, Picard group
Since projective space is an integral scheme of finite type, smooth over the base, we have four different isomorphic characterizations of the Picard group. It is the group of invertible sheaves (lines bundles) with tensor product, up to isomorphism  . It is isomorphic to the Cartier class group
. It is isomorphic to the Cartier class group  of Cartier divisors modulo principal divisors, which is isomorphic to the sheaf cohomology group
of Cartier divisors modulo principal divisors, which is isomorphic to the sheaf cohomology group  . It is the Class group
. It is the Class group  of Weil divisors modulo principal divisors.
of Weil divisors modulo principal divisors.
Any hypersurface  of degree
of degree  in projective
in projective  -space is linearly equivalent to the Weil divisor
-space is linearly equivalent to the Weil divisor 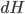 , where
, where ![H = \{[x_0:\cdots:x_n] \in \mathbb{P}^n : x_0=0\}](http://www.konradvoelkel.com/wp-content/plugins/latex/cache/tex_a38a8711275f22a1fadbec00555d223c.gif) is a (generic) hyperplane. In particular, all hyperplanes are linearly equivalent to each other. The degree of
is a (generic) hyperplane. In particular, all hyperplanes are linearly equivalent to each other. The degree of  is
is  , so the degree homomorphism
, so the degree homomorphism  is an isomorphism. In particular,
is an isomorphism. In particular,  is non-trivial. One can show
is non-trivial. One can show  by first proving
by first proving  for
for  the divisor of a non-zero rational function
the divisor of a non-zero rational function  and then writing
and then writing  for
for  some rational functions, so
some rational functions, so  .
.
The line bundles on  , for
, for  a field, are generated (up to isomorphism) by the tautological bundle
a field, are generated (up to isomorphism) by the tautological bundle 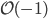 , its dual
, its dual 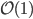 and their tensor powers
and their tensor powers  , which are all called twisting sheaves. The usual isomorphism
, which are all called twisting sheaves. The usual isomorphism  identifies
identifies  with
with 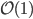 .
.
Chow ring
The Chow ring  of
of  is the graded ring whose
is the graded ring whose  -th graded component is the Chow group
-th graded component is the Chow group  of codimension
of codimension  cycles up to rational equivalence, with ring structure coming from the intersection product. Here, we consider Chow groups with integer coefficients.
cycles up to rational equivalence, with ring structure coming from the intersection product. Here, we consider Chow groups with integer coefficients.
Let us first look at  . Can we come up with any cycles, hopefully non-trivial ones? In dimension
. Can we come up with any cycles, hopefully non-trivial ones? In dimension 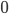 , that is codimension
, that is codimension  , we have the points
, we have the points  which are all rationally equivalent, since any two points
which are all rationally equivalent, since any two points  in
in 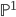 can be joined by a
can be joined by a 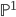 via the map
via the map ![\phi : [x_0:x_1] \mapsto [x_0p_0+x_1q_0,x_0p_1+x_1q_1]](http://www.konradvoelkel.com/wp-content/plugins/latex/cache/tex_dbb3f7b283b5bc423c0c815c434c6d32.gif) (check
(check ![\phi([1:0]) = p, \phi([0:1]) = q](http://www.konradvoelkel.com/wp-content/plugins/latex/cache/tex_9a99da650057a31123a8260d11f7d035.gif) ). In dimension
). In dimension  , that is codimension
, that is codimension 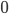 , there is
, there is 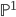 and that's the only closed subvariety, since
and that's the only closed subvariety, since 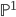 is irreducible. In higher or lower codimensions, there is nothing.
is irreducible. In higher or lower codimensions, there is nothing.
The trick that shows that two points on 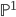 are rationally equivalent actually works for hyperplanes in
are rationally equivalent actually works for hyperplanes in  , and we have seen (in the section above) that one can show (using linear equivalence of divisors) that these are all classes of cycles. Since rational equivalence of codimension 1 cycles coincides with linear equivalence of divisors, this shows that
, and we have seen (in the section above) that one can show (using linear equivalence of divisors) that these are all classes of cycles. Since rational equivalence of codimension 1 cycles coincides with linear equivalence of divisors, this shows that ![A^\bullet(\mathbb{P}^1) = \mathbb{Z}[H]/(H^2)](http://www.konradvoelkel.com/wp-content/plugins/latex/cache/tex_92a1cd29847497adb60b503ddd6f5fc6.gif) , for
, for  the class of a hyperplane
the class of a hyperplane ![\{[x_0:x_1] : x_0=0\}](http://www.konradvoelkel.com/wp-content/plugins/latex/cache/tex_7911ebc8ba4a8e781f6896a73a7b12fe.gif) (in fact, a point).
(in fact, a point).
The structure of  looks less clear at first, but one can show that it is generated by any codimension
looks less clear at first, but one can show that it is generated by any codimension  linear subspace via the following "excision lemma":
linear subspace via the following "excision lemma":
Lemma: Let  be a closed immersion,
be a closed immersion,  the open complement, then the sequence
the open complement, then the sequence  is exact for all
is exact for all  (where the arrows are pushforward by
(where the arrows are pushforward by 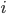 and
and 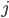 , so we need to take the grading by dimension).
, so we need to take the grading by dimension).
We apply this with  ,
,  ,
,  a hyperplane, and then
a hyperplane, and then  . Then we use
. Then we use  for
for  to get that
to get that  is a surjection. In fact, also
is a surjection. In fact, also  is a surjection for
is a surjection for  , and because of
, and because of  we can use induction.
A small remark: the excision lemma can be improved to a long exact localization/Gysin sequence for higher Chow groups, and the next term on the left would be
we can use induction.
A small remark: the excision lemma can be improved to a long exact localization/Gysin sequence for higher Chow groups, and the next term on the left would be  , which gives a much smoother proof. The localization sequence, on the other hand, is very very hard to prove (at least that's what Voevodsky writes, so I believe it).
To see that there are no relations in
, which gives a much smoother proof. The localization sequence, on the other hand, is very very hard to prove (at least that's what Voevodsky writes, so I believe it).
To see that there are no relations in  (for
(for  ), i.e.
), i.e. ![A^k(\mathbb{P}^n) = \mathbb{Z} [H^k]](http://www.konradvoelkel.com/wp-content/plugins/latex/cache/tex_23b5cb75b3d03cffb88e1b3f46f4055a.gif) with
with  the class of a codimension
the class of a codimension  linear subspace, we look at the cases
linear subspace, we look at the cases  (since the case
(since the case  is clear and we have seen the case
is clear and we have seen the case  above, that was the divisor-setting). Any relation would be of the form
above, that was the divisor-setting). Any relation would be of the form ![d H^k = \sum n_i [div(r_i)]](http://www.konradvoelkel.com/wp-content/plugins/latex/cache/tex_e044cca0d1010afcbdde5d2d1c929516.gif) for
for  some rational functions. Let
some rational functions. Let  and
and  the projection to a linear
the projection to a linear  -dimensional subspace disjoint from
-dimensional subspace disjoint from 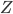 . Then
. Then  is proper, so there is proper pushforward
is proper, so there is proper pushforward  which can not annull
which can not annull  because of compatibility with the degree morphism
because of compatibility with the degree morphism  (and
(and  has degree
has degree  over
over  ), but has to annul
), but has to annul ![\sum n_i [div(r_i)]](http://www.konradvoelkel.com/wp-content/plugins/latex/cache/tex_e9ec16ca416928cbe30bc11a61ccae03.gif) .
.
We see that two hyperplanes in  in general position intersect to a linear subspace of codimension
in general position intersect to a linear subspace of codimension 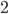 , and in general
, and in general  , so we have
, so we have
![A^\bullet(\mathbb{P}^n) = \mathbb{Z}[H]/(H^{n+1})](http://www.konradvoelkel.com/wp-content/plugins/latex/cache/tex_79a48e8e2703d5c86ee092cf5194d5b1.gif) .
.
Algebraic K-Theory
From the general theory, we can use smoothness of  over a perfect field
over a perfect field  to deduce that the Chern character with rational coefficients
to deduce that the Chern character with rational coefficients  is an isomorphism. I think this also works for
is an isomorphism. I think this also works for  over
over  , since only regularity is used. However, the rational coefficients are quite unsatisfying. At least from
, since only regularity is used. However, the rational coefficients are quite unsatisfying. At least from ![K^\bullet(\mathbb{P}^n_k)_{\mathbb{Q}} \simeq \mathbb{Q}[H]/(H^{n+1})](http://www.konradvoelkel.com/wp-content/plugins/latex/cache/tex_e104a3ed6fd63e162a9aec6542806781.gif) we can guess how
we can guess how  might look like. Or can we? Actually it is way more complicated than the rationalized picture, and I think the general answer is still unknown!
might look like. Or can we? Actually it is way more complicated than the rationalized picture, and I think the general answer is still unknown!
Serre proved a theorem, that every coherent sheaf on  admits a surjective map of some
admits a surjective map of some  for positive
for positive  . This shows that
. This shows that 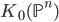 is generated by the set of all
is generated by the set of all 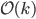 . Furthermore, one can show that there is a relation in
. Furthermore, one can show that there is a relation in  between any set of
between any set of  coherent sheaves on
coherent sheaves on  , by analyzing the Koszul complex on
, by analyzing the Koszul complex on  .
.
For  a rank
a rank  vector bundle on a quasiprojective variety
vector bundle on a quasiprojective variety  , one can look at the projective bundle
, one can look at the projective bundle  which is fiber-wise a projective space of the fiber. On the total space
which is fiber-wise a projective space of the fiber. On the total space  one has canonically the tautological bundle and its tensor powers
one has canonically the tautological bundle and its tensor powers  , which generate (for
, which generate (for 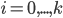 )
)  . One can take a vector bundle
. One can take a vector bundle  , pull it back to
, pull it back to  and twist it (i.e. tensor it with some
and twist it (i.e. tensor it with some  ). This gives functors
). This gives functors  .
.
The projective bundle theorem for algebraic K-Theory says that these functors  induce an equivalence
induce an equivalence  and
and  is a ring isomorphism.
is a ring isomorphism.
If we apply this to a trivial rank  vector bundle
vector bundle  , where
, where  , we see that
, we see that ![K_\bullet(\mathbb{P}^k_X) \simeq K_\bullet(X)[z]/[z^{k+1}]](http://www.konradvoelkel.com/wp-content/plugins/latex/cache/tex_77b79d5ec593125bd6e35d83f1668e65.gif) .
.
In particular, ![K_\bullet(\mathbb{P}^k) \simeq K_\bullet(\mathbb{Z})[z]/[z^{k+1}]](http://www.konradvoelkel.com/wp-content/plugins/latex/cache/tex_f8b03429e73545db82fe548a219573ab.gif) . But the higher algebraic K-groups of the integers are not known! One might naively guess that it becomes better by taking a field as base, but fields (even algebraically closed ones) have a very rich higher K-theory, too.
. But the higher algebraic K-groups of the integers are not known! One might naively guess that it becomes better by taking a field as base, but fields (even algebraically closed ones) have a very rich higher K-theory, too.
Still, the projective bundle theorem shows us that the K-Theory of projective space isn't really complicated, since all the complexity lies in the K-Theory of the base.
Some afterthoughts
By the way, I realise during writing this that I would love to hear something about other isomorphism invariants I'm missing, like the Kodaira dimension, existence of a spin structure on the associated complex manifold, volume of the Fubini-Study metric, geodesic completeness, Lusternik-Schnirelman category, whatever... I fell in love with the idea of computing everything of  . Please tell me your favourite isomorphism invariant of
. Please tell me your favourite isomorphism invariant of  or
or  or
or  in the comments!
in the comments!
