Model structures on simplicial presheaves
Friday, November 23rd, 2012 | Author: Konrad Voelkel
This is a very short notice to memorize some of the various model structures on simplicial presheaves in a systematic way.
[UPDATE 2013-03-06] I gave a talk in our working group seminar about model structures on simplicial presheaves, homotopy sheaves and h-principles [/UPDATE]
Preliminaries
If you get left/right, cofibration/fibration, injective/projective wrong, there is a quick fix: In the model category axioms, the factorizations (axiom M5) factor a morphism into a cofibration followed by a fibration (in both factorizations), so the cofibration is left and the fibration is right. In the lifting axiom (M4), the cofibration is on the left column of the diagram, the fibration on the right (at least in the more popular textbooks). Some people use a hookrightarrow for injections, some use these arrows for cofibrations; some people use a twoheadrightarrow for surjections, others use these for fibrations. In the most popular model structure on topological spaces, for a relative CW complex  the inclusion
the inclusion  is an injection and a cofibration as well (these memorization tricks work for me; do you have more?).
is an injection and a cofibration as well (these memorization tricks work for me; do you have more?).
To get a homotopy category of a category, one just has to define weak equivalences. To pimp up a class of weak equivalences, one has to define fibrations or cofibrations -- but then the third class is actually fixed by these data, via the lifting axiom. Of course, one has to show in each case that one really gets a model structure.
There is one a priori choice to fix (for our purposes): That of a model structure on simplicial sets. Choose a different (but Quillen-equivalent) one and you get something different in all what follows, but it will be Quillen-equivalent. Quillen equivalence implies isomorphic homotopy categories but it is much stronger than that. I prefer the Kan model structure, where a map is a weak equivalence iff its geometric realization is a weak homotopy equivalence and a simplicial set is fibrant iff it is Kan (i.e. has the horn filling property) and a map is a cofibration iff it is a monomorphism (i.e. level-wise injection).
(This model category is Quillen equivalent to the Serre model structure on topological spaces via the adjunction of geometric realization and singular complex).
Simplicial presheaves admit some interesting subcategories: simplicial sets can be embedded as constant sheaves (hence sets can be embedded) and presheaves can be embedded as simplicially constant simplicial presheaves (hence the base category can be embedded, via the Yoneda embedding).
If we consider simplicial presheaves on an arbitrary category, there are just the global structures (see below). I'm more interested in the special case where one looks at simplicial presheaves or simplicial sheaves on a Grothendieck site (say, on the big Zariski site, or on the category of open subsets of a manifold). In simple terms, I want to consider situations where the sheaf property (that allows uniquely gluing sections that match on intersections) is meaningful. In less simple terms, I will talk about coverings  , which you can (if you don't know about Grothendieck topologies) take to be open coverings, i.e.
, which you can (if you don't know about Grothendieck topologies) take to be open coverings, i.e.  and the maps
and the maps  are inclusions of open subsets (or anything isomorphic to that).
are inclusions of open subsets (or anything isomorphic to that).
If one has different Grothendieck topologies on a category, this yields different "local" model structures (see below).
Global structures
Before we go simplicial or sheafy, on any presheaf category with values in a model category there are the global injective and the global projective model structure. The word refers to what part of the structure is done object-wise: in the injective structure, the cofibrations are taken object-wise, in the projective structure, the fibrations are taken object-wise. In both structures the weak equivalences are taken object-wise, which means (to spell it out once) that a morphism of presheaves  is a weak equivalence in the global model structures if for all objects
is a weak equivalence in the global model structures if for all objects  the morphism
the morphism  of sections is a weak equivalence.
of sections is a weak equivalence.
There is an abundance of synonyms for model cats on simplicial presheaves.
global injective == "Heller",
global projective == "Bousfield-Kan".
One can also find various intermediate model structures that interpolate between the global injective and the global projective model structure. From tradition some people leave out the adjective injective/projective, then they talk about the injective model structure most of the time.
Cech localization
To compute Cech cohomology of a presheaf  over a covering
over a covering  can be formulated by the Cech nerve of the covering, which is the simplicial object
can be formulated by the Cech nerve of the covering, which is the simplicial object  which consists of
which consists of  in degree
in degree  , then
, then  in degree
in degree 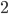 and so on (n-fold intersections in degree
and so on (n-fold intersections in degree 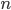 ) with the obvious simplicial structure. The
) with the obvious simplicial structure. The 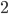 -truncation of this Cech nerve shows up in the sheaf axiom, where we apply
-truncation of this Cech nerve shows up in the sheaf axiom, where we apply  to it and impose that
to it and impose that  is a limit of this diagram. Actually, one can take the limit over
is a limit of this diagram. Actually, one can take the limit over  , that makes no difference.
, that makes no difference.
It is a basic fact about gluing schemes that, for a Zariski cover  of a scheme
of a scheme  the morphism
the morphism  is an isomorphism (one could even use that to define schemes, by imposing the condition on a presheaf or locally ringed space
is an isomorphism (one could even use that to define schemes, by imposing the condition on a presheaf or locally ringed space  that there exists an open affine cover such that the colimit over the Cech nerve is isomorphic to
that there exists an open affine cover such that the colimit over the Cech nerve is isomorphic to  ).
).
If we look at simplicial presheaves with any model structure (for example, a global one), we can form not only  but also
but also  , the homotopy colimit. One can construct this homotopy colimit in a way that there is a morphism
, the homotopy colimit. One can construct this homotopy colimit in a way that there is a morphism 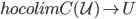 , but that morphism needn't be an isomorphism, and it will in general not be a weak equivalence in the model structure. The homotopy-theoretic analogue of the sheaf axiom reads as: a (simplicial) presheaf is called a hosheaf (synonym: has the Brown-Gersten property) if for all objects
, but that morphism needn't be an isomorphism, and it will in general not be a weak equivalence in the model structure. The homotopy-theoretic analogue of the sheaf axiom reads as: a (simplicial) presheaf is called a hosheaf (synonym: has the Brown-Gersten property) if for all objects  and all coverings
and all coverings  of
of  the simplicial set
the simplicial set  is the homotopy colimit of
is the homotopy colimit of  . In model-categorical terminology, a hosheaf is a local object for the morphisms
. In model-categorical terminology, a hosheaf is a local object for the morphisms 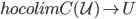 , since it "sees them" as weak equivalences. Note that a hosheaf needn't be a sheaf and vice versa, although a presheaf can be a sheaf and a hosheaf at the same time.
, since it "sees them" as weak equivalences. Note that a hosheaf needn't be a sheaf and vice versa, although a presheaf can be a sheaf and a hosheaf at the same time.
The left local Bousfield localization of the global injective model structure along the Cech coverings, i.e. the morphisms 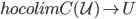 , is called the injective Cech model structure. The left local Bousfield localization of the global projective model structure along the Cech coverings is called the projective Cech model structure. During the process of left local localization, the (hint: left) cofibrations remain unchanged, while the class of weak equivalences is enhanced (here: by all
, is called the injective Cech model structure. The left local Bousfield localization of the global projective model structure along the Cech coverings is called the projective Cech model structure. During the process of left local localization, the (hint: left) cofibrations remain unchanged, while the class of weak equivalences is enhanced (here: by all 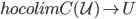 ), so the fibrations need to change, too: in the local structure, there are less fibrations (since they have more conditions to fulfill in the lifting axiom).
), so the fibrations need to change, too: in the local structure, there are less fibrations (since they have more conditions to fulfill in the lifting axiom).
Synonyms:
injective Cech == "Cech-Heller",
projective Cech == "Cech-Bousfield-Kan".
Characteristics of the Cech model structures: Sheafification is a weak equivalence. One can compute Cech cohomology in this model structure. One can, however, not compute higher sheaf cohomology, in general, as the coverings might not be "fine enough".
Localization at hypercovers
The Verdier hypercovering theorem (in a simple form) states: For  an object of the site and
an object of the site and  a sheaf of abelian groups on the site, the sheaf cohomology can be computed via hypercovers, i.e. the colimit indexed by the poset of all hypercovers
a sheaf of abelian groups on the site, the sheaf cohomology can be computed via hypercovers, i.e. the colimit indexed by the poset of all hypercovers  of
of  over the groups
over the groups  is isomorphic to
is isomorphic to  .
.
A hypercover is a generalization of Cech nerves of covers, where one allows the step  to be replaced by a coproduct of coverings of the
to be replaced by a coproduct of coverings of the 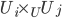 , and then at the next step, the threefold intersection (fiber product, really) is replaced by a covering of it. This allows for more refinement of the steps. For example, in scheme theory the intersection of two affine sets in an affine open cover of a scheme is not affine, in general, but since it is a scheme you can cover it by affines, which results in a hypercover by affines. The Cech nerve of a covering may not have that property and it may be possible that there is no covering such that the Cech nerve has that property. That is (roughly) why one needs hypercovers. Over very nice sites (such as the étale site), Cech nerves of coverings actually suffice to compute sheaf cohomology.
, and then at the next step, the threefold intersection (fiber product, really) is replaced by a covering of it. This allows for more refinement of the steps. For example, in scheme theory the intersection of two affine sets in an affine open cover of a scheme is not affine, in general, but since it is a scheme you can cover it by affines, which results in a hypercover by affines. The Cech nerve of a covering may not have that property and it may be possible that there is no covering such that the Cech nerve has that property. That is (roughly) why one needs hypercovers. Over very nice sites (such as the étale site), Cech nerves of coverings actually suffice to compute sheaf cohomology.
The left local Bousfield localization of the global injective model structure along all hypercoverings, i.e. the morphisms  , is called the injective local model structure. The left local Bousfield localization of the global projective model structure along all hypercoverings is called the projective local model structure.
, is called the injective local model structure. The left local Bousfield localization of the global projective model structure along all hypercoverings is called the projective local model structure.
Synonyms:
injective local == "Jardine",
projective local == "Blander".
If people talk about "the" local model structure, most of the time they talk about the injective local model structure. Sometimes, the local injective structure is even called "standard" model structure. If it is not specified whether someone considers a global or a local model structure, most likely it will be a local model structure (but you can't be sure).
Characteristics of the local model structures: they are further localizations of the Cech model structures, so in particular the sheafification is a weak equivalence. If the site has enough points (i.e. sheaf isomorphism can be tested on stalks), a morphism in the local model structures is a weak equivalence iff it is a weak equivalence on stalks. This property is sometimes used as definition.
The injective local model structure was defined by Joyal on the (sub)category of simplicial sheaves. Sheafification and the forgetful functor define a Quillen equivalence between the injective local structure on simplicial presheaves and the injective local structure on simplicial sheaves. Some people call both structures "Jardine", some call both "Joyal".
If one has two Grothendieck topologies, one strictly finer than the other (e.g. the étale topology on schemes is finer than the Zariski topology), then the local model structures can be compared, since any fine weak equivalence will be a coarse weak equivalence. The global model structures are just a special case of this comparison, since they are the local model structures for the coarsest of all Grothendieck topologies.
A¹-homotopy theory
Morel and Voevodsky used the big Nisnevich site on (smooth projective) schemes over a field  to define the A¹-homotopy theory. More precisely, they consider the local injective model category of simplicial presheaves on the Nisnevich site and localize it at the object
to define the A¹-homotopy theory. More precisely, they consider the local injective model category of simplicial presheaves on the Nisnevich site and localize it at the object  , hence the name. The Nisnevich topology lies between the Zariski and the étale topology, so one can define analogous model categories for the Zariski and étale topology and compare (which is how one can prove some things).
, hence the name. The Nisnevich topology lies between the Zariski and the étale topology, so one can define analogous model categories for the Zariski and étale topology and compare (which is how one can prove some things).
Localizing at an object makes all morphisms with fiber or cofiber this object weak equivalences. In particular the projection map  becomes a weak equivalence in this localization.
becomes a weak equivalence in this localization.
Morel and Voevodsky have described their model category in a more general setting: on any site with an interval. The result is not just any model category, but a proper simplicial one (so you can calculate stuff).
If you do the Morel-Voevodsky construction on topological spaces (with jointly surjective local homeomorphisms as coverings, for example) with the interval ![[0,1]](http://www.konradvoelkel.com/wp-content/plugins/latex/cache/tex_ccfcd347d0bf65dc77afe01a3306a96b.gif) , you get some model structure on the simplicial presheaves (in their theory actually sheaves, but that's equivalent) with
, you get some model structure on the simplicial presheaves (in their theory actually sheaves, but that's equivalent) with ![[0,1]](http://www.konradvoelkel.com/wp-content/plugins/latex/cache/tex_ccfcd347d0bf65dc77afe01a3306a96b.gif) a contractible object. The homotopy category is equivalent to the classical homotopy category of topological spaces, and in some sense it is the canonical model-categorical construction of it.
a contractible object. The homotopy category is equivalent to the classical homotopy category of topological spaces, and in some sense it is the canonical model-categorical construction of it.
By the way: Jardine has a new book, Local Homotopy Theory.
