Monday, May 04th, 2015 | Author: Konrad Voelkel

Here are slides containing more content than a blackboard talk I gave in May 2015 in Freiburg:
Git versioning (why and how) for Mathematicians
Git Logo by Jason Long is licensed under the Creative Commons Attribution 3.0 Unported License.
Category: English, Not Mathematics | One Comment
Tuesday, January 27th, 2015 | Author: Konrad Voelkel

I was asked to give a talk about division algebras (purpose and classification). This is a rough overview of it, mostly learned from the book of Springer and Veldkamp "Octonions, Jordan Algebras and Exceptional Groups" and the book of Lam "Noncommutative Rings". The book "Numbers" by Ebbinghaus et al. was also nice to read along for references.
We will look mostly at finite dimensional (not neccesarily associative) division algebras over the real numbers.
Instead of these rather loose notes, you may prefer to look at my texed notes in this pdf file.
Continue reading «Classification of Division Algebras»
Category: English, Mathematics | Comments off
Monday, October 27th, 2014 | Author: Konrad Voelkel

A classic class of "math problem" is the continuation of integer sequences from a finite sample (usually at the beginning). For example:
Continue 2,4,6,8,...
To which the solution is often supposed to be 10,12,14, and so on.
The problem, as any mathematician knows, is that there is not the one solution. In fact, given any set of finite numbers one could just talk about the sequence that starts like that and continues with zeroes only, that's a perfectly valid sequence. Of course, one should really figure out the rule behind the finitely many numbers, but there are always many possible choices. The game is not to find any sensible rule, but to find the rule the designer had in mind. It's more about testing your knowledge of culture than an honest test of mathematical ability (or anything else).
But there is a way to fix this.
Continue reading «Continuing Integer Sequences»
Category: English, Mathematics | Comments off
Tuesday, March 25th, 2014 | Author: Konrad Voelkel

In this lightheaded post (written long time ago) I want to share with you some fundamental adjunctions that are the "source" of various other adjunctions that pop up all over in mathematics (well, at least all over algebraic topology).
claimtoken-5399a1ffcd81c
Continue reading «Fundamental Adjunctions»
Category: English, Mathematics | Comments off
Monday, February 24th, 2014 | Author: Konrad Voelkel

This is about the mathematical concepts of a "magma", a "loop" and a "monoid", which are descriptions of certain properties that the combining of things may enjoy.
Continue reading «Magmas, Loops and Monoids»
Category: English, Mathematics | Comments off
Thursday, February 13th, 2014 | Author: Konrad Voelkel
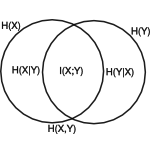
Back in 2010 I had a series of posts going about questions in information theory that arose from a 2-week seminar with a bunch of students coming from various scientific disciplines (a wonderful event!). Here I picked those that I still find particularly compelling:
- Is the mathematical definition of Kullback-Leibler distance the key to understand different kinds of information?
- Can we talk about the total information content of the universe?
- Is hypercomputation possible?
- Can we tell for a physical system whether it is a Turing machine?
- Given the fact that every system is continually measured, is the concept of a closed quantum system (with unitary time evolution) relevant for real physics?
- Can we create or measure truly random numbers in nature, and how would we recognize that?
- Would it make sense to adapt the notion of real numbers to a limited (but not fixed) amount of memory?
- Can causality be defined without reference to time?
- Should we re-define “life”, using information-theoretic terms?
What do you think?
Category: English, Questions in Information Theory | Comments off





