Magmas, Loops and Monoids
Monday, February 24th, 2014 | Author: Konrad Voelkel
This is about the mathematical concepts of a "magma", a "loop" and a "monoid", which are descriptions of certain properties that the combining of things may enjoy.
One of the most basic notions of mathematics are sets with subsets and powersets. From these, one can define a binary relation between sets  and
and  to be a subset of
to be a subset of  and then a map from
and then a map from  to
to  to be a binary relation between
to be a binary relation between  and
and  which is left-total (each element of
which is left-total (each element of  is related to at least one element of
is related to at least one element of  ) and right-unique (aka "functional", each element of
) and right-unique (aka "functional", each element of  is related to at most one element of
is related to at most one element of  ).
).
Magmas
A binary operation by  on
on  is a map
is a map  . A binary operation of
. A binary operation of  on itself is called an inner binary operation on
on itself is called an inner binary operation on  . A magma
. A magma  is a set
is a set  with an inner binary operation
with an inner binary operation  .
.
Examples of magmas: the natural numbers with addition  (but not the natural numbers with subtraction) and the set of words over an alphabet, with concatenation. The former is a special case of the latter if we encode numbers unary, i.e.
(but not the natural numbers with subtraction) and the set of words over an alphabet, with concatenation. The former is a special case of the latter if we encode numbers unary, i.e. 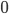 is the empty word,
is the empty word,  is just
is just  (
(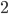 is
is  ) and every other number
) and every other number 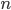 is a word of length
is a word of length 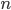 consisting only of
consisting only of  s. The alphabet is
s. The alphabet is  and
and 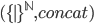 is essentialy the same as
is essentialy the same as  .
.
Concatenation can be done in more than one dimension, i.e. we can consider not only words 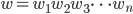 over an alphabet
over an alphabet  (such that
(such that  ) with concatenation ("horizontal composition"), but 2-dimensional words composed of letters
) with concatenation ("horizontal composition"), but 2-dimensional words composed of letters  , such that each
, such that each  with fixed
with fixed 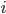 and varying
and varying 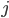 is an ordinary word, and each
is an ordinary word, and each  with fixed
with fixed 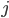 and varying
and varying 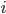 is a word written vertically. Such a 2-dimensional word has a "rectangular shape". The set of all 2-dimensional words over an alphabet
is a word written vertically. Such a 2-dimensional word has a "rectangular shape". The set of all 2-dimensional words over an alphabet  has two magma structures (horizontal composition and vertical composition) and it can be interesting how they interact.
has two magma structures (horizontal composition and vertical composition) and it can be interesting how they interact.
A classical example of a set with two magma structures is the set of loops in a pointed topological magma (continuous paths from the basepoint to the basepoint), with one operation given by the pointwise operation of the topological magma and the other given by concatenation of loops.
Other magmas: the natural numbers with multiplication, the natural numbers with exponentiation  , the complex numbers with multiplication, the octonions with multiplication, the sedenions with multiplication. If you haven't seen the octonions or sedenions before, look up the Cayley–Dickson construction in Wikipedia.
, the complex numbers with multiplication, the octonions with multiplication, the sedenions with multiplication. If you haven't seen the octonions or sedenions before, look up the Cayley–Dickson construction in Wikipedia.
A magma homomorphism  is a map
is a map  such that
such that  . The unary encoding of natural numbers discussed above is a magma isomorphism
. The unary encoding of natural numbers discussed above is a magma isomorphism  .
.
A magma operation  of a magma
of a magma  on a set
on a set  is a binary operation
is a binary operation  of
of 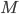 on
on  that is compatible with the magma operation
that is compatible with the magma operation  , i.e.
, i.e.  .
.
There are some elementary properties one can study for any magma  one encounters:
one encounters:
- Associativity: Is
 ?
? - Neutral Elements:
 ?
? - Units:
 ?
? - The dual magma
 with
with 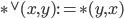 .
. - Commutativity: Is
 ?
? - Solvability of Equations: Does there exist a unique inner binary operation
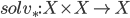 such that
such that  ?
?
A magma with the property that equations of the form 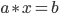 and
and 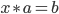 are uniquely solvable is called a quasigroup. A loop is a quasigroup that posesses a neutral element.
are uniquely solvable is called a quasigroup. A loop is a quasigroup that posesses a neutral element.
An associative magma is sometimes called a semigroup, although that word is also used for monoids, which are associative magmas that posess a neutral element, i.e. an element  such that
such that  and
and  are both equal to the identity map.
are both equal to the identity map.
Groups can be defined as monoids in which every element is a unit, i.e. every 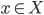 has an inverse element
has an inverse element  which satisfies
which satisfies  and
and  . Groups can also be defined as associative loops.
. Groups can also be defined as associative loops.
Loops
A Loop is a quasigroup with a neutral element, but it needn't be associative or commutative. In a loop, every element has a left-inverse and a right-inverse, since  and
and  are uniquely solvable, but unlike a group, these one-sided inverses don't coincide in general.
are uniquely solvable, but unlike a group, these one-sided inverses don't coincide in general.
In a loop  , the left-associator
, the left-associator 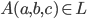 of three elements
of three elements  , defined by
, defined by  , measures how non-associative the loop is (together with the right-associator).
, measures how non-associative the loop is (together with the right-associator).
A quasigroup  has the Moufang property (or satisfies the Moufang identity) if
has the Moufang property (or satisfies the Moufang identity) if  , which is a weak form of associativity. The Moufang property implies that there exists a neutral element (so the quasigroup is a loop, after all): since
, which is a weak form of associativity. The Moufang property implies that there exists a neutral element (so the quasigroup is a loop, after all): since  is uniquely solvable and
is uniquely solvable and 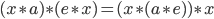 is uniquely solvable, we have
is uniquely solvable, we have 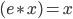 , for all
, for all  , so
, so  is left-neutral. Now take
is left-neutral. Now take 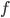 defined by
defined by  , which can be shown by the same method to be right-neutral, so we conclude with
, which can be shown by the same method to be right-neutral, so we conclude with  .
.
A loop that enjoys the Moufang property is called a Moufang loop. In a Moufang loop, left-inverses coincide with right-inverses. In particular, the left-associator and the right-associator coincide (but the associator is still non-trivial in general).
The nonzero quaternions with quaternion multiplication form a non-commutative associative loop. The nonzero octonions form a non-associative Moufang loop. In general, the set of invertible elements of an alternative algebra forms a Moufang loop. The integers with subtraction form a loop with neutral element 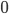 that does not have the Moufang property.
that does not have the Moufang property.
Moufang's theorem states that the subloop generated by any two elements of a Moufang loop is an associative loop, i.e. a group. This theorem makes working with loops a lot more convenient.
Monoids
A monoid is an associative magma with a neutral element, but it needn't be commutative or have any inverses. A monoid homomorphism is a magma homomorphism that maps neutral elements to neutral elements.
An archetypical monoid is the set of endomorphisms of some thing, since composition of morphisms is required to be associative and there is the identity morphism. In other words, any monoid 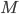 can be seen as a category with one object
can be seen as a category with one object  and
and  and vice versa. Observe that a group in this formalism is a category with one object such that all morphisms are invertible.
and vice versa. Observe that a group in this formalism is a category with one object such that all morphisms are invertible.
This points to an obvious generalization of monoids: categories. The corresponding generalization of groups is called groupoid.
To every commutative monoid 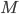 one can associate an abelian group
one can associate an abelian group 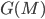 such that the monoid homomorphisms into any other abelian group
such that the monoid homomorphisms into any other abelian group  are in bijection with the group homomorphisms
are in bijection with the group homomorphisms  . This can be done by the construction familiar from building integers
. This can be done by the construction familiar from building integers  out of natural numbers
out of natural numbers  and is called the Grothendieck group. Other prominent examples of this construction lie in the fundamentals of K-Theory.
and is called the Grothendieck group. Other prominent examples of this construction lie in the fundamentals of K-Theory.
The Eckmann-Hilton argument
The Eckmann-Hilton theorem states for a set  with two inner binary operations
with two inner binary operations  that have a neutral element
that have a neutral element  and distribute over each other, i.e.
and distribute over each other, i.e.  , that the two operations actually coincide, their neutral elements coincide and that this operation is associative and commutative.
, that the two operations actually coincide, their neutral elements coincide and that this operation is associative and commutative.
The classical application of the theorem is the case of the monoid of homotopy classes of loops of an H-space, which shows that, up to homotopy, composition of loops is the same as multiplication of loops. As a corollary, all higher homotopy groups 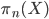 of a topological space
of a topological space  , for
, for  , are abelian.
, are abelian.
It is very nice to work out the Eckmann-Hilton argument as an exercise given a few hints: visualize the two operations as horizontal and vertical composition and look at expressions of the form  .
.
