I want to discuss the elementary basics of Thom spaces of vector bundles. To start, I explain general one-point compactification and a different construction on vector spaces, then I do it for vector bundles to define the Thom space. I also discuss suspension of topological spaces and how adding a trivial vector space (or bundle) corresponds to suspension under the forming of Thom spaces.

Motto: (Thom space:Suspension)::(Vector bundle:Trivial bundle) or

"Thom spaces are twisted suspensions"

Honestly, I really want to talk about algebraic (motivic) Thom spaces some day, but these are some preliminaries to understand what's going on, so I want to get this out first.

One-point compactification

In what follows, X should be a topological space.
The one-point (or Alexandroff) compactification of X is defined as the set $X\sqcup \{\infty\}$ and the topology consisting of all open sets of X and, in addition, for all compact subsets $K \subset X$ the set $(X\setminus K)\sqcup \{\infty\}$ (i.e. complements of compacta are open).
This is indeed a compact space, since every open cover must contain at least one open set containing $\infty$, thus being the complement of a compact set K which is covered by all other sets in the cover, from which we can choose finitely many.
If X is a locally compact Hausdorff space, the one-point compactification is again Hausdorff (prove by separating any point from the infinite point).

If V is a finite dimensional real vector space, we can choose a norm and talk about the open unit disk (all vectors of norm smaller than 1) and its boundary, the unit sphere (all vectors of norm exactly 1). The open unit disk is homeomorphic to V itself and its boundary is like a smaller version of the "boundary at infinity" which is not part of V. To adjoin one point to V and glue it along this "boundary at infinity" to V (the one-point compactification) is the same as smashing the unit sphere together to one point, keeping it glued to the open unit disk as it was. The result, in both cases, is a sphere. It is most easily imaginable with $V=\mathbb{R}^2$ and the unit disk in the euclidean norm, embedded in $\mathbb{R}^3$ as the lower hemisphere of a 2-sphere.

If $p : E \to X$ is a vector bundle over a topological space X, we have the fibers $p^{-1}(x) \simeq V$, which are isomorphic to a vector space $V$ (though not by a fixed isomorphism). On each vector bundle one can choose continuously a so-called metric, which is a scalar product on each fiber. This in turn gives a norm and we can proceed by taking the sub-bundle consisting of the unit disk in each fiber. It is no longer a vector bundle, but merely a fiber bundle with fiber a disk. By smashing together the boundary (or taking the one-point compactification) we get a sphere bundle over X. It is most easily imaginable with $X = S^1$ and $V = \mathbb{R}$, so that the sphere bundle is exactly $S^1 \times S^1$ (a torus).

Thom spaces

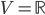From the sphere bundle we can proceed further, by introducing a continuous choice of basepoint on the fiber, and then smashing all these together to one point (for the whole bundle). The result is a space with a map to X, but the fibers are never disjoint, as the basepoint is the same in each fiber. Taking the picture of $X=S^1$ and $V=\mathbb{R}$, the torus can be given a continuous choice of basepoint by taking the "inner" $S^1$ and pinching it together gives a torus whose inner hole became a singular point. A neat way to visualize that space is to start with an $S^2$ and then identify the top and the bottom point (-1 and +1 in some coordinate system). The result can already be called a Thom space, namely the Thom space of the vector bundle.

A better construction of the Thom space just takes the closed disk bundle associated to the vector bundle and smashes together the whole subspace of the unit sphere bundle inside. To do that, one doesn't need to introduce any basepoint choices (and it is maybe less clear at first sight).

A non-trivial example of a Thom space which is still somewhat visualizable, is obtained from the Möbius bundle. The Möbius bundle is a rank 1 vector bundle over $S^1$ which is twisted, in the following sense:
Any vector bundle can be trivialized over small open sets, which are segments of the circle. Since the circle is compact, a finite number of such overlapping segments suffice. Given a vector v in the fiber over the point 1 in the circle, we can extend it to a constant section over such a small segment where the bundle is trivial. On the overlap to the next segment, we can extend to the whole segment, still locally constant. Going around the circle once, we end up with another vector in the fiber over the point 1, but not necessarily the same. For trivial vector bundles, it will be the same (exercise: prove that), but for the Möbius bundle it will be exactly -v, the additive inverse. It turns out that you can repeat the same procedure with -v and get v, so going around twice the Möbius bundle behaves like going around once a trivial bundle. That's how it's "twisted".

The Thom space of the Möbius bundle looks like a Möbius strip with border (there is only one) smashed together to one point. This space is homeomorphic to the real projective plane, so we can summarize:

$$Th(\text{Moebius}\to S^1) \simeq \mathbb{R}P^2$$

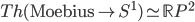
We will come back to this example at the very end of this post.

Suspension

From a topological space X one can construct its suspension, which is "just" $\Sigma X := X \wedge S^1$, which is, by definition, $X \times S^1$ with the subspaces $\ast \times S^1$ and $X \times \ast$ smashed together to one point. Sometimes, this is called reduced suspension, and the ordinary suspension is the space $SX := (X \times [0,1])/(x,0)\sim (x',0), (x,1)\sim (x',1)$ which looks like taking X and suspending it, literally, at the top and the bottom, but has no natural basepoint any longer. The reduced suspension is obtained from the unreduced suspension by collapsing the space $\{\ast\} \times [0,1]$ to one point, which is then the natural basepoint.

For many spaces X (e.g. compact manifolds), the quotient map from unreduced to reduced suspension is even a homotopy equivalence. You might visualize the situation most easily for $X=S^1$, where the unreduced suspension is a quotient of $S^1 \times [0,1]$ which is quite obviously homeomorphic to $S^2$ and you can also "see" how the reduced suspension is homotopy equivalent to $S^2$ as well.

It is a general fact that supension of spheres gives you higher-dimensional spheres. Denoting by $\Sigma^n X$ the n-fold suspension $\Sigma \Sigma \cdots \Sigma X$, we can state

$$\Sigma^n S^k = S^{n+k}.$$

Another example is given by the point: suspending a point is $\Sigma\text{pt} = \text{pt} \times [0,1] \simeq [0,1]$, which is homotopy equivalent to a point. So in the homotopy-sense, suspending a point gives a point. This is different from suspending two points, since the space $\text{pt} \sqcup \text{pt}$ is the same as $S^0 = \{-1,1\}$, the zero-sphere (i.e. vectors of norm 1 in the real line).

You can change the description of the suspension via $X \times [0,1]$ slightly:
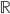Take $X \times \mathbb{R}$ and inside $\mathbb{R}$ the segment $[-1,1]$ (which is, by the way, the same as the closed unit ball in $\mathbb{R}^1$). Now you can smash $X \times \{-1\}$ together to one point and also smash $X \times \{+1\}$ together to one (distinct) point, voilà there is the (unreduced) suspension of $X$.

Adding a trivial bundle

Suppose you have a vector bundle $E \to X$ over some topological space X. Then you can ask whether E is trivial (i.e. $E \simeq X \times V$, and the map $E \to X$ is just the projection onto the first product factor, where $V$ is the vector space which is the fiber of $E \to X$) and which rank E has (i.e. which dimension the fiber $V$ has).

Any space X can be considered as a trivial vector bundle of rank 0 over X, by the identity map $X \to X$. Over any space you can take the trivial rank n bundle $X \times \mathbb{R}^n \to X$, which is just the projection to the first product factor. We want to call this trivial rank n bundle just $\mathcal{E}^n \to X$ or even $\mathcal{E}^n$.

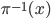One can add two vector bundles $\pi: E \to X$ and $\nu: E' \to X$ by defining the space $E \oplus E'$ and the projection $E \oplus E' \to X$ fiber-wise: the space $E \oplus E'$ is the disjoint union over all $\pi^{-1}(x) \oplus \nu^{-1}(x)$, with the projection mapping an element of $\pi^{-1}(x)$ to x and similarly an element of $\nu^{-1}(x)$ to x. From local trivializations of E and E' you can write down a local trivialization of $E \oplus E'$ and from this you can define the topology on the total space $E \oplus E'$.

This, altogether, enables us to add trivial bundles to a given space or vector bundle. The Thom space of the trivial rank n bundle is $Th(\mathcal{E}^n) = (X \times D^n)/(X \times S^n)$, where $D^n \subset \mathbb{R}^n$ is the closed unit ball, with boundary $S^n$. We will prove that this Thom space is $Th(\mathcal{E}^n) = S^n$ and even more:
If we start from a vector bundle $E \to X$, we can add a trivial rank n bundle $E \oplus \mathcal{E}^n \to X$ and look what happens with the Thom space of E, or in other words, how $Th(E)$ relates to $Th(E \oplus \mathcal{E}^n)$. The answer is

$$Th(E \oplus \mathcal{E}^n) \simeq \Sigma^n Th(E).$$

We can prove this by induction, showing just

$$Th(E \oplus \mathcal{E}^1) \simeq \Sigma Th(E),$$

since adding a rank n trivial bundle is the same as adding a rank 1 trivial bundle n times.

The left hand side is obtained from $E \times \mathbb{R}$ by looking at the subspace of norm less or equal than 1 vectors, and quotienting out the boundary sphere. Since we're talking about finite dimensional vector spaces, we can switch to any other norm, and obtain the same topological space, so we choose the norm where the closed unit ball in $E \times \mathbb{R}$ is given by the closed unit ball in E (denoted D) times $[-1,1]$, i.e.

$$Th(E \oplus \mathcal{E}^1) = (D \times [-1,1])/((D \times \{-1,1\}) \cup (\partial D \times [-1,1]))$$

This is obviously equivalent to

$$(D \times [0,1])/((D \times \{0,1\}) \cup (\partial D \times [0,1])),$$

which can be re-written as

$$\left((D/\partial D) \times [0,1]\right) / (D/\partial D \times \{0,1\}),$$

which is nothing but the reduced suspension (up to homotopy equivalence) of $Th(E)$.

That is basically what I wanted to explain.

If you're convinced that spheres are important spaces to look at (since you can build CW complexes out of spheres, they are), you should now look at Thom spaces as an important way to build twisted spheres. While any vector bundle over a point is trivial, hence gives an ordinary sphere as Thom space, this is no longer true in the relative setting.