Thom spaces
Wednesday, June 13th, 2012 | Author: Konrad Voelkel

I want to discuss the elementary basics of Thom spaces of vector bundles. To start, I explain general one-point compactification and a different construction on vector spaces, then I do it for vector bundles to define the Thom space. I also discuss suspension of topological spaces and how adding a trivial vector space (or bundle) corresponds to suspension under the forming of Thom spaces.
Motto: (Thom space:Suspension)::(Vector bundle:Trivial bundle) or
"Thom spaces are twisted suspensions"
Honestly, I really want to talk about algebraic (motivic) Thom spaces some day, but these are some preliminaries to understand what's going on, so I want to get this out first.
Category: English, Mathematics | 2 Comments










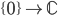
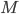

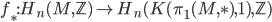
![[M] \in H_n(M,\mathbb{Z})](https://www.konradvoelkel.com/wp-content/plugins/latex/cache/tex_6fd228685037a445f5a86e7d621040ec.gif)
![f_\ast([M]) \neq 0 \in H_n(K(\pi_1(M,\ast),1),\mathbb{Z})](https://www.konradvoelkel.com/wp-content/plugins/latex/cache/tex_625b0d4c3630329950c69a5f6cb9f126.gif)