Aspherical manifolds
Wednesday, August 10th, 2011 | Author: Konrad Voelkel
In this post I want to sketch the idea of aspherical manifolds - manifolds which don't admit higher homotopically non-trivial spheres - and the related concepts of Eilenberg-MacLane-spaces and classifying spaces for groups.
Definition
A topological space 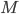 is called aspherical if all higher homotopy groups vanish, i.e.
is called aspherical if all higher homotopy groups vanish, i.e. 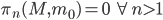 where
where 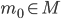 is an arbitrary basepoint and
is an arbitrary basepoint and 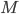 is assumed to be connected.
is assumed to be connected.
Since manifolds admit universal covers, you could equivalently define a manifold to be aspherical if and only if its universal cover is contractible.
Just one example illustrating how rich this class of spaces is:
Metric spaces that are of non-positive curvature (i.e. locally CAT(0)-spaces), for example the Bruhat-Tits building of a simple algebraic group over a field with a discrete valuation, are aspherical.
A good survey on aspherical manifolds was given by Wolfgang Lück.
Definition
A connected topological space  is called Eilenberg-MacLane-space for a group
is called Eilenberg-MacLane-space for a group  and a natural number n if its nth homotopy group is exactly
and a natural number n if its nth homotopy group is exactly  and all other homotopy groups vanish, i.e.
and all other homotopy groups vanish, i.e.
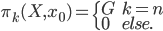
Then one calls  also
also  .
.
The standard examples of  spaces are
spaces are  , which is a
, which is a  and
and  , which is a
, which is a  .
.
Of course, every  is aspherical and every aspherical space is a
is aspherical and every aspherical space is a  for
for  being its fundamental group.
being its fundamental group.
One can also define a functorial construction of a  which gives a CW-complex model for every group
which gives a CW-complex model for every group  and transforms group homomorphisms into continuous maps of spaces.
and transforms group homomorphisms into continuous maps of spaces.
For this, we need the functorial nerve construction.
Definition
The nerve 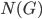 of a (discrete) group
of a (discrete) group  is the simplicial
is the simplicial  -set with n-simplices being the (n+1)-fold cartesian product of sets
-set with n-simplices being the (n+1)-fold cartesian product of sets  , face maps just omitting one factor in the cartesian product, degeneracies adding the identity element of
, face maps just omitting one factor in the cartesian product, degeneracies adding the identity element of  in one factor.
in one factor.
By construction, seen as a discrete simplicial group,  embeds into
embeds into 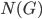 as the 0-skeleton. Observe that
as the 0-skeleton. Observe that 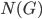 is contractible, since every n-simplex
is contractible, since every n-simplex  is the face of
is the face of  which also has the face
which also has the face  , thus allowing to move every point to the identity
, thus allowing to move every point to the identity  which is just a degeneracy of
which is just a degeneracy of  .
.
The group  acts diagonally on
acts diagonally on 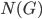 , i.e. it acts on an n-simplex by the formula
, i.e. it acts on an n-simplex by the formula 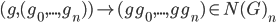 . This action is compatible with face and degeneracy maps, thus making
. This action is compatible with face and degeneracy maps, thus making 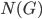 into a simplicial
into a simplicial  -set. The action is free, i.e. no two elements of
-set. The action is free, i.e. no two elements of  operate in the same way.
operate in the same way.
Using the nerve construction, we now define the classifying space:
Definition
The classifying space 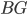 of a group
of a group  is the quotient
is the quotient  of the geometric realisation
of the geometric realisation  of the nerve construction by the group action described above. It turns out that
of the nerve construction by the group action described above. It turns out that  operates on
operates on  like a deck transformation group, thus giving
like a deck transformation group, thus giving 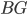 the structure of a CW-complex with universal cover
the structure of a CW-complex with universal cover  and fundamental group
and fundamental group  .
.
A group homomorphism  gives rise to a morphism of simplicial sets
gives rise to a morphism of simplicial sets  by pointwise application. Geometric realisation is also functorial, and due to $\phi$ being a homomorphism, the continuous map
by pointwise application. Geometric realisation is also functorial, and due to $\phi$ being a homomorphism, the continuous map 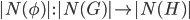 descends to a continuous map of classifying spaces
descends to a continuous map of classifying spaces  .
.
If you are not into simplicial sets and geometric realisation, you can look for a more hands-on approach in Hatcher's book "Algebraic Topology", on page 87, chapter 1.B, more specifically Example 1B.7 on page 89.
Now back to our first definitions: An aspherical manifold is just a manifold which happens to be a  for
for  being its fundamental group. The classifying space is just an explicit (functorial!) construction which gives a
being its fundamental group. The classifying space is just an explicit (functorial!) construction which gives a  for every group
for every group  (although most authors would call our
(although most authors would call our 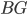 just one explicit model for
just one explicit model for 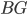 ...).
...).
One would like to work only with CW-complexes, if possible, since they allow induction over the skeleton and cell-by-cell arguments. Is every manifold homeomorphic to a CW-complex - long time ago there was the "Hauptvermutung" (main conjecture) which asked this, but it's wrong. While compact manifolds admit a homotopy equivalent CW-model (by Kirby and Siebenmann), this is not true for topological manifolds in general. Let us look what one could do with a CW-model:
Proposition
Let  be a connected CW complex and
be a connected CW complex and  be a
be a  (for example, your favourite aspherical manifold). Let
(for example, your favourite aspherical manifold). Let 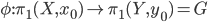 be a homomorphism of groups. Then there is a continuous map
be a homomorphism of groups. Then there is a continuous map 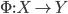 mapping
mapping  to
to 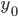 which induces
which induces  on fundamental groups; furthermore, the map
on fundamental groups; furthermore, the map 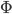 is unique up to homotopy relative
is unique up to homotopy relative  .
.
The proof of this proposition goes roughly like that: First, let 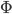 map
map  to
to 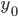 . Now, for each 1-cell
. Now, for each 1-cell 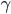 , take a representative of
, take a representative of ![\phi([\overline{\gamma}]) \in \pi_1(Y,y_0)](https://www.konradvoelkel.com/wp-content/plugins/latex/cache/tex_d668edd8fdbd8e3b2cba1dcd11957d28.gif) to define
to define 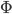 on
on 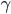 . Then one has to extend the map given on the 1-skeleton to
. Then one has to extend the map given on the 1-skeleton to  , using the fact that
, using the fact that  has no higher homotopy.
has no higher homotopy.
Corollary
Every two CW-complexes 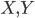 which are both
which are both  -spaces are homotopy equivalent ("of the same homotopy type").
-spaces are homotopy equivalent ("of the same homotopy type").
To prove this, just take isomorphisms  and
and  and define
and define 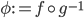 which gives
which gives 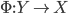 with inverse up to homotopy given by
with inverse up to homotopy given by  induced by
induced by  .
.
This justifies that every invariant of 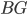 that depends only on the homotopy type, is actually an invariant of
that depends only on the homotopy type, is actually an invariant of  - a very useful idea. One can define group homology with integer coefficients of
- a very useful idea. One can define group homology with integer coefficients of  by the formula
by the formula  .
.
One drawback of the classifying space via the nerve construction is that it is usually very large - there are simplices in arbitrary high dimensions. For example, the circle  , given as example of a
, given as example of a  , is much more efficient than
, is much more efficient than 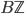 .
.
Of course, talking about aspherical manifolds, we don't want to forget the manifold structure. Given a group  , one could expect that many non-homeomorphic aspherical manifolds with fundamental group
, one could expect that many non-homeomorphic aspherical manifolds with fundamental group  exist - even many non-homotopy equivalent ones. At least we can say that such non-homotopy equivalent aspherical manifolds are not of CW homotopy type. There is an old conjecture on this theme:
exist - even many non-homotopy equivalent ones. At least we can say that such non-homotopy equivalent aspherical manifolds are not of CW homotopy type. There is an old conjecture on this theme:
Conjecture (Borel)
Let M and N be closed aspherical manifolds, and let  be a homotopy equivalence. Then
be a homotopy equivalence. Then  is homotopic to a homeomorphism.
is homotopic to a homeomorphism.
Together with the result of Kirby and Siebenmann (that every closed manifold is of CW homotopy type), this would imply that closed aspherical manifolds are classified by their fundamental group up to homeomorphism.
The property that every homotopy equivalence is homotopic to a homeomorphism is called
