Classifying Riemann surfaces
Wednesday, October 21st, 2009 | Author: Konrad Voelkel
In this post, I will sketch a classification of Riemann surfaces.
For those who haven't heard about the subject before, there is an introduction. For the impatient, look at the bottom of the post, where I have written a very short summary.
Table of contents:
- Definitions
- Examples and counter-examples
- Topological classification, the genus
- Digression about algebraic field extensions
- Biholomorphic classification via universal covering deck transformations
- Brief discussion of Gaussian curvature and conformal geometry
- Summary
Introduction
At first, a definition: A Riemann surface is a connected complex manifold of (complex) dimension 1 (so real dimension 2, which qualifies it as a surface). A compact Riemann surface is a Riemann surface which is compact as a topological space.
At first, let's think only about orientable surfaces. Orientability means that the orientation double cover is trivial (not simply-connected), or equivalently, the tangent bundle (or sheaf, if you prefer) admits a global section. In simple terms, orientable means you can take an orientation with you, walk around the surface, return where you were first and the orientation is still the same.
It turns out that every complex manifold is orientable as real manifold, so a Riemann surface is always orientable as a real surface (and this is what we care about for the moment).
Some simple examples of Riemann surfaces:
- the complex plane
 itself
itself - the upper half plane
 (also called the hyperbolic disc; it's biholomorphic to the open unit disc)
(also called the hyperbolic disc; it's biholomorphic to the open unit disc) - Complex projective space of one dimension
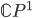 which is topologically a sphere
which is topologically a sphere  , called Riemann sphere
, called Riemann sphere - A complex torus
 , that is the quotient of the complex plane
, that is the quotient of the complex plane  by a lattice
by a lattice  with some
with some 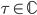 , so we have
, so we have 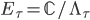
Some simple counter-examples:
- The moebius strip is not orientable (so it admits no complex structure).
- Complex projective space modulo action of
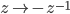 is a real manifold, but no longer a complex one.
is a real manifold, but no longer a complex one.
So we know what we're talking about. Now what kind of classification do we search? The "best" classification would be one up to biholomorphism, but let's see how far we can get. First, we can seperate different surfaces by their topology. This is a good approximation because each biholomorphism is a homeomorphism.
Topological classification
Note that, topologically, all tori  are homeomorphic. Their complex structure is different and depends on
are homeomorphic. Their complex structure is different and depends on  which can always be chosen to lie in
which can always be chosen to lie in  , the complex upper half plane. This variable
, the complex upper half plane. This variable  is called the modulus of
is called the modulus of  .
.
However, 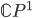 and
and  are not homeomorphic, their genera are different. The genus is a topological invariant which completely classifies the compact (orientable real) surfaces up to homeomorphism. This can be shown by proving that each such surface admits a triangulation and then showing each triangulation is homeomorphic to a standard genus
are not homeomorphic, their genera are different. The genus is a topological invariant which completely classifies the compact (orientable real) surfaces up to homeomorphism. This can be shown by proving that each such surface admits a triangulation and then showing each triangulation is homeomorphic to a standard genus  triangulation. Roughly speaking, the genus is "the number of holes" inside the surface. One can "mathematise" this definition by speaking about loops non-homotopic to the constant loop, which leads to a discussion of the fundamental group
triangulation. Roughly speaking, the genus is "the number of holes" inside the surface. One can "mathematise" this definition by speaking about loops non-homotopic to the constant loop, which leads to a discussion of the fundamental group 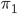 . The study of fundamental groups is also necessary to understand holomorphic (branched) coverings, which are used in the biholomorphic classification theory.
. The study of fundamental groups is also necessary to understand holomorphic (branched) coverings, which are used in the biholomorphic classification theory.
Biholomorphic classification
There are other surfaces than 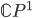 and tori
and tori  . The famous Riemann Mapping Theorem tells us, that the only simply connected Riemann surfaces are
. The famous Riemann Mapping Theorem tells us, that the only simply connected Riemann surfaces are  and
and 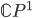 .
.
Digression about algebraic field extensions
(You don't have to read this)
So the only compact surface without holes is 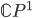 . This is interesting, because by definition a meromorphic function on a surface
. This is interesting, because by definition a meromorphic function on a surface  is a holomorphic map
is a holomorphic map 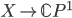 . The collection of all meromorphic functions on a surface
. The collection of all meromorphic functions on a surface  is written
is written  , it's always a field, called the function field of
, it's always a field, called the function field of  . If there is an element
. If there is an element  in
in  , it is always a branched covering. There is a theorem, that shows each Riemann surface admits a non-constant meromorphic function. This leads to the conclusion, that the map
, it is always a branched covering. There is a theorem, that shows each Riemann surface admits a non-constant meromorphic function. This leads to the conclusion, that the map 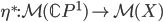 which sends each
which sends each  to
to 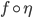 is an algebraic field extension of degree
is an algebraic field extension of degree  , where
, where  is the degree of the covering
is the degree of the covering  . Since the meromorphic functions on
. Since the meromorphic functions on 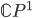 are just the rational functions
are just the rational functions  (a transcendence degree 1 extension of the complex numbers), each compact Riemann surface has a function field which is an algebraic field extension of
(a transcendence degree 1 extension of the complex numbers), each compact Riemann surface has a function field which is an algebraic field extension of  .
.
The other way works, too: To each algebraic field extension of  we can define a corresponding compact Riemann surface.
we can define a corresponding compact Riemann surface.
Every compact Riemann surface can be embedded in complex projective space of at most dimension 3. With Chow's Theorem, we get the surprising statement that every compact Riemann surface is algebraic.
Universal coverings
We can understand a Riemann surface by it's coverings, since it will be a quotient of the covering. To be more specific: for each covering  , the space
, the space  is biholomorphic to the quotient of
is biholomorphic to the quotient of  with respect to the transformation subgroup which commutes with the projection
with respect to the transformation subgroup which commutes with the projection 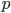 . This transformation subgroup is called the group of deck transformations (it's similar to the Galois group of a field extension). There are some theorems about that:
. This transformation subgroup is called the group of deck transformations (it's similar to the Galois group of a field extension). There are some theorems about that:
A surface  which is covered by
which is covered by 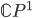 is already biholomorphic to
is already biholomorphic to 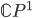 .
.
A surface covered by  is biholomorphic either to
is biholomorphic either to 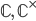 or a torus. On the other hand, every torus is covered by
or a torus. On the other hand, every torus is covered by  . For surfaces with universal covering space
. For surfaces with universal covering space  , the situation is more complicated. For example, one can show that every hyper-elliptic surface is covered by
, the situation is more complicated. For example, one can show that every hyper-elliptic surface is covered by  .
.
Automorphisms of simply connected surfaces
Now we can realise every Riemann surface as quotient of the simply connected spaces, since every surface admits a universal covering, which is by definition a simply connected Riemann surface. In order to do the classification, we have to study the automorphism groups of the simply connected surfaces and their subgroups.
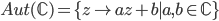 (Affine translations)
(Affine translations)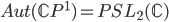 (Möbius transformations)
(Möbius transformations) (Möbius transformations preserving the unit disc)
(Möbius transformations preserving the unit disc)
Curvature
One can show that each Riemann surface admits a Riemannian metric because they are all paracompact. Luckily, this metric is unique up to conformal equivalence for a given complex structure. Every such metric is equivalent to one with a constant Gaussian curvature either  or
or 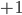 .
.
Short summary
Every Riemann surface is the quotient of a free, proper holomorphic group action on its universal covering, which is one of the simply connected surfaces 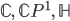 . The complete list:
. The complete list:
- Elliptic surfaces - constant Gauss curvature
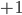
- Genus 0: only the Riemann sphere
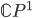
- Genus 1 or higher: None.
- Genus 0: only the Riemann sphere
- Parabolic surfaces - constant Gauss curvature
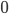
- Genus 0: only the complex plane

- Genus 1: either
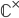 or a torus
or a torus  , where the tori biholomorphism classes are in one-to-one correspondence to the elements of their moduli space
, where the tori biholomorphism classes are in one-to-one correspondence to the elements of their moduli space  .
. - Genus 2 or higher: None.
- Genus 0: only the complex plane
- Hyperbolic surfaces - constant Gauss curvature

- Genus 0: only the hyperbolic disc

- Genus 1 and higher: quotients of
 by a Fuchsian group. Sadly, further classification is difficult (but at least for compact surfaces, we can apply the theory of field extensions sketched above)
by a Fuchsian group. Sadly, further classification is difficult (but at least for compact surfaces, we can apply the theory of field extensions sketched above) - All genus > 1 and especially the so-called hyperelliptic surfaces belong to this class.
- Genus 0: only the hyperbolic disc
I wrote this because I couldn't find a quick overview of the classification, with enough but not too much detail, on the web. If you find mistakes or have any questions, don't hesitate to contact me and/or write a comment :-)
UPDATE: this is the conformal classification. There are various other classifications, see Solomentsevs explanations here and Krushkal's explanations here.
