The four functors of Grothendieck in examples
Tuesday, May 01st, 2012 | Author: Konrad Voelkel
This post will discuss the definition of the four functors "pushforward"  , "pullback"
, "pullback"  , "pushforward with compact support"
, "pushforward with compact support"  and "exceptional pullback"
and "exceptional pullback"  of sheaves of abelian groups, associated to a continuous morphism
of sheaves of abelian groups, associated to a continuous morphism  of topological spaces
of topological spaces  and
and  . Then we will look at maps
. Then we will look at maps  which are open immersions or closed immersions, and calculate in the example of
which are open immersions or closed immersions, and calculate in the example of  and its closed complement
and its closed complement 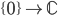 exactly what happens. This is intended to give some intuition what the general four functor calculus is about.
exactly what happens. This is intended to give some intuition what the general four functor calculus is about.
The four functor formalism arises as part of the six functor formalism (add Hom and Tensor to make it six) in certain (co)homological set-ups. Where I encountered it first was in a paper I tried to read, about the stable motivic homotopy category, but most likely you'll see this stuff in papers dealing with perverse sheaves or motives and their realisations.
Disclaimer: We'll stay in the topological category for this post, i.e. the objects are topological spaces and the morphisms continuous maps. Sheaves are ordinary sheaves of abelian groups (no fancy Grothendieck topology necessary here), not  -modules of some sort. However, the discussion doesn't change too much if you translate into the algebraic category, so this should be a good exercise for the bored reader.
-modules of some sort. However, the discussion doesn't change too much if you translate into the algebraic category, so this should be a good exercise for the bored reader.
Pushforward
Pushforward of sheaves is straightforward: given a space  , a sheaf
, a sheaf  on
on  and a continuous map
and a continuous map  , the sheaf
, the sheaf  on
on  should be a sheaf that does on open subsets
should be a sheaf that does on open subsets  what
what  had done on the corresponding open subsets of
had done on the corresponding open subsets of  , i.e.
, i.e.  . Check that this definition gives again a sheaf. Observe that the constant map
. Check that this definition gives again a sheaf. Observe that the constant map  yields
yields 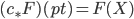 , so
, so 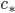 is almost the global section functor and we should think of any
is almost the global section functor and we should think of any  as some kind of generalized global section functor.
as some kind of generalized global section functor.
Pullback
I want to define the pullback functor  as the left adjoint to
as the left adjoint to  . Of course, I have to show existence.
. Of course, I have to show existence.
If  would be an open embedding, we would have
would be an open embedding, we would have  open in
open in  for all open subsets
for all open subsets  of
of  , and it would be natural to define
, and it would be natural to define  . To see that we indeed have a left adjoint by this definition is up to you, but it fails for a general
. To see that we indeed have a left adjoint by this definition is up to you, but it fails for a general  , since
, since  needn't be open in general.
needn't be open in general.
So, given a sheaf  on
on  I define a new presheaf on
I define a new presheaf on  by
by 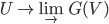 , where the limit ranges over all open subsets
, where the limit ranges over all open subsets  such that
such that  contains
contains  . By this "trick" we circumvent the given problem (and introduce new behaviour) and it turns out that this is a correct definition, in the technical sense that we really have found a left adjoint to
. By this "trick" we circumvent the given problem (and introduce new behaviour) and it turns out that this is a correct definition, in the technical sense that we really have found a left adjoint to  .
.
Proof of the adjunction 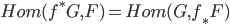 :
:
for an open subset  of
of  , a homomorphism from
, a homomorphism from 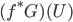 to
to  is just a homomorphism from
is just a homomorphism from  to
to  and a homomorphism from
and a homomorphism from  to
to  is just a homomorphism from
is just a homomorphism from  to
to 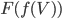 . So you see, if we have homomorphisms
. So you see, if we have homomorphisms  for all
for all  , this gives in the limit homomorphisms
, this gives in the limit homomorphisms  .
.
For the other direction, observe that if we have homomorphisms  for all
for all  , we certainly have this for all
, we certainly have this for all 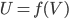 , where the limit is just
, where the limit is just  , i.e. where we have just
, i.e. where we have just  .
.
Pushforward with compact support
We have already seen how pushforward generalizes global sections. As global sections give (as derived functor) cohomology of sheaves, there is a global section with compact support functor, which gives cohomology with compact support. For the locally constant sheaf  this gives back "singular" cohomology with compact support, as it appears in Poincaré duality. I will explain this in some more detail now, although I won't explain how to move from global sections to cohomology.
this gives back "singular" cohomology with compact support, as it appears in Poincaré duality. I will explain this in some more detail now, although I won't explain how to move from global sections to cohomology.
Poincaré duality states, for a smooth compact complex n-dimensional manifold X

and if X is not compact, there is still Poincaré duality:

where
 is the cohomology with compact support,
is the cohomology with compact support,which is related to the functor of global sections with compact support,
just as ordinary cohomology is related to the ordinary global section functor.
The functor of global sections with compact support  is defined as
is defined as

By analogy, we define the pushforward with compact support  as a subfunctor of
as a subfunctor of  (which just means that
(which just means that  will be a subsheaf of
will be a subsheaf of  for every
for every  , which in turn just means that
, which in turn just means that  is a subset of
is a subset of  for every open set
for every open set  ).
).

This really gives a sheaf and for
 the constant map to a point,
the constant map to a point,the values are exactly
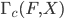 .
.
An example:
Let  be an open embedding
be an open embedding 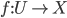 , then
, then  is just the "extension by zero", i.e. the stalks at all points of
is just the "extension by zero", i.e. the stalks at all points of  are just the same as those of
are just the same as those of  , and all other/new stalks (over
, and all other/new stalks (over  ) are plain
) are plain  .
.
Another example:
Let  be a proper map
be a proper map 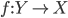 , then
, then 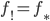 , as you can see from the definition.
, as you can see from the definition.
A comprehensive example:
If  can be factored into
can be factored into 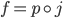 with
with 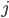 an open embedding and
an open embedding and 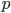 proper, we have
proper, we have 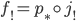 , which gives a very explicit description of
, which gives a very explicit description of  .
.
Exceptional inverse image
We define a functor  called
called  , if it exists. We should say straightforward, that it doesn't exists, in general, on the level of sheaves and this is one of the things that makes working with complexes of sheaves necessary (in fact, the derived category).
, if it exists. We should say straightforward, that it doesn't exists, in general, on the level of sheaves and this is one of the things that makes working with complexes of sheaves necessary (in fact, the derived category).
However, for innocent maps  , we can actually define a functor that is right adjoint to
, we can actually define a functor that is right adjoint to  and thus deserves to be called
and thus deserves to be called  .
.
For f an open embedding 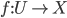 , we have just
, we have just  , i.e. the functor
, i.e. the functor  is the left adjoint to
is the left adjoint to  and also the right adjoint to
and also the right adjoint to  .
.
The proof is similar to the proof of the adjointness of  with
with  , so I leave it out.
, so I leave it out.
Now I want to make clear why a right adjoint to  doesn't exist (on the level of sheaves) in general, for categorical reasons.
doesn't exist (on the level of sheaves) in general, for categorical reasons.
Every left adjoint functor preserves colimits, since an adjunction like
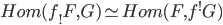
means that one can compute
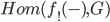 as the Hom-functor
as the Hom-functor  , where colimits in the first argument are obviously preserved (now apply Yoneda lemma). There we use that the Hom-functor turns colimits in its first argument into limits, which doesn't work with limits, so left adjoints needn't preserve limits. Exercise: apply the same reasoning to see that right adjoints preserve limits.
, where colimits in the first argument are obviously preserved (now apply Yoneda lemma). There we use that the Hom-functor turns colimits in its first argument into limits, which doesn't work with limits, so left adjoints needn't preserve limits. Exercise: apply the same reasoning to see that right adjoints preserve limits.
Now being right-exact is a special case of preserving colimits, since it means to preserve cokernels (which are special colimits). Clearly,  is not right-exact, since it has cohomology: let
is not right-exact, since it has cohomology: let  be a compact space and
be a compact space and  the constant map to a point. Then for
the constant map to a point. Then for  to be right-exact, the cohomology on
to be right-exact, the cohomology on  must vanish.
must vanish.
The salvation consists of enlarging the category of sheaves to the category of chain complexes of sheaves, only to make it smaller again by introducing the appropriate definition of morphisms, which in the end gives what is called the  exists.
exists.
Concrete examples for four functors
Let us look at the embedding  and its closed complement
and its closed complement  .
.
First we will look at a skyscraper sheaf on  with stalk some abelian group
with stalk some abelian group  over
over 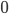 . We denote the skyscraper sheaf by
. We denote the skyscraper sheaf by  . By definition, we have
. By definition, we have 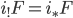 a skyscraper sheaf with stalk
a skyscraper sheaf with stalk  over
over 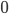 . Now
. Now  , since
, since  throws away all information from the stalk over
throws away all information from the stalk over 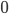 .
.
Okay, let's look at a local system on  , i.e. a locally constant sheaf
, i.e. a locally constant sheaf  .
.
This is the same data (an equivalent category) as the monodromy representation of the fundamental group, in this case  .
.
We have as 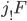 a sheaf with stalks just
a sheaf with stalks just  where
where  , and
, and 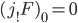 , since every section with compact support is away from an arbitrarily small ball around the origin.
, since every section with compact support is away from an arbitrarily small ball around the origin.
The sheaf 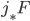 has the same stalks
has the same stalks  where
where  but it has a new one at the origin, given by the usual stalk-limit-formula you would write down - and in general, this is non-zero.
but it has a new one at the origin, given by the usual stalk-limit-formula you would write down - and in general, this is non-zero.
Cleary  vanishes, since
vanishes, since 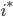 picks the stalk at the origin and throws away everything else. Of course,
picks the stalk at the origin and throws away everything else. Of course,  contains exactly the "new" stalk which might be interesting.
contains exactly the "new" stalk which might be interesting.
Thinking about it, the sheaves  and
and  are both zero, by the same argument we had for
are both zero, by the same argument we had for 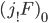 . Here you can also use the adjunction for reasoning!
. Here you can also use the adjunction for reasoning!
Last words
The nice thing about this setting is that it generalizes to give the following:
Take  a closed subspace in
a closed subspace in  and
and  its open complement, then you have an open embedding
its open complement, then you have an open embedding 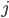 and a closed embedding
and a closed embedding 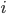 which behave very much like our
which behave very much like our 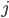 and
and 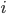 from the last examples. It presents the category of sheaves on
from the last examples. It presents the category of sheaves on  as an extension of the sheaves on
as an extension of the sheaves on  by the sheaves on
by the sheaves on  . The same happens for the derived category. The magic word for this situation is "Recollement".
. The same happens for the derived category. The magic word for this situation is "Recollement".

2018-03-26 (26. March 2018)
In 4th line of your "Pullback" section where the notion is defined do you mean to write: "(f^*G)(U):= G(f(U)" where G is a sheaf of abelian groups over Y?
2018-03-26 (26. March 2018)
Corrected, thanks!