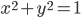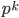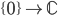Given a vector bundle E-->X of rank r+1 one can take the projective space of lines in each fiber, which results in a projective bundle P(E)-->X. A projective bundle formula for a functor F from spaces to rings tells us that F(P(E)) is a free F(X)-module of rank r.

In this post I look at some computations around projective bundle formulae for the Chow ring, the algebraic K-Theory and the (Chow) motive of some spaces, in particular flag varieties. We recover some results from the previous posts on cohomology, cycles & bundles and motive of projective space.

Continue reading «Motives of Projective Bundles»

A vector bundle is a morphism that looks locally on the target like a product of the target with a vector space.

We will call the target space the base and the space of definition the total space. The preimage of a point of the base is called the fiber.

Is that the correct mathematical definition? It doesn't mention what kind of spaces we look at, what kind of morphism I'm talking about, what the product is, locally in which sense, vector space over which field, do we allow infinite dimension, ... so it's not a mathematical definition in the pedantic sense. I will give you pedantic definitions in this article, just to satisfy my need to write down what I consider to be a good terminology.

Continue reading «What is ... a vector bundle?»

You probably know the integers $\mathbb{Z}$ which can be defined as the Grothendieck group of the monoid of natural numbers $\mathbb{N}$ which exists by the axioms of Zermelo-Fraenkel set theory and probably in almost all other axiom systems as well. So the integers are a quite fundamental object in mathematics (did I really just argue for that? Well, now I did).

It is also natural to look what one can derive from the integers. In this short article I want to describe some rings that can be obtained from the integers by quotients, subgroups, products, and in general (co)limits and combinations thereof. The purpose might not be so clear, but it was a by-product of other investigations and I hope it could be interesting to say something about some concrete rings.

Continue reading «Some Interesting Rings»

I must admit that I have a weak background in elementary number theory. A few weeks ago I wanted to count the number of points of the affine circle $x^2+y^2=1$ over finite fields, by counting the point of the completed curve and the points at infinity. There one needs to decide whether a finite field with $p^k$ elements contains roots of -1 or not.

Continue reading «Zeta of x²+y²=1 over finite fields»

I want to discuss the elementary basics of Thom spaces of vector bundles. To start, I explain general one-point compactification and a different construction on vector spaces, then I do it for vector bundles to define the Thom space. I also discuss suspension of topological spaces and how adding a trivial vector space (or bundle) corresponds to suspension under the forming of Thom spaces.

Motto: (Thom space:Suspension)::(Vector bundle:Trivial bundle) or

"Thom spaces are twisted suspensions"

Honestly, I really want to talk about algebraic (motivic) Thom spaces some day, but these are some preliminaries to understand what's going on, so I want to get this out first.

Continue reading «Thom spaces»

This post will discuss the definition of the four functors "pushforward" $f_\ast$, "pullback" $f^\ast$, "pushforward with compact support" $f_{!}$ and "exceptional pullback" $f^{!}$ of sheaves of abelian groups, associated to a continuous morphism $f : X \to Y$ of topological spaces $X$ and $Y$. Then we will look at maps $f$ which are open immersions or closed immersions, and calculate in the example of $\mathbb{C}^\times \to \mathbb{C}$ and its closed complement $\{0\} \to \mathbb{C}$ exactly what happens. This is intended to give some intuition what the general four functor calculus is about.

Continue reading «The four functors of Grothendieck in examples»