We will investigate the notion of cellular objects in a model category; today: the classical case of CW-complexes in the model category of topological spaces with Serre-fibrations as fibrations.

A CW complex is a certain kind of topological space, together with a CW structure, which is a description how to glue the space from spheres (or from affine spaces, if you prefer), called the cells. The acronym CW stands for "closure finite, weak topology", which I will explain soon. CW complexes are a class of spaces broader than simplicial complexes, and they are still combinatorial in nature.

You can read definitions in the Wikipedia, I will only present the inductive definition here:

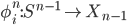A CW complex $X$ consists of n-skeleta $X_n$ which are Hausdorff topological spaces, together with attaching maps in each degree n, that are maps $\phi_i^n : S^{n-1} \to X_{n-1}$ indexed by $i \in I_n$, such that $X_{n} = X_{n-1} \cup_{\bigvee_{i \in I_n} \phi_i} \bigvee_{i \in I_n} D^{n}$. By definition, $X_{-1} := \emptyset$ and $S^{-1} = \emptyset$.
The map $\phi_i^n$ describes how to attach an affine space (the "cell") of dimension $n$, considered as unit ball $D^{n}$, along its boundary $S^{n-1}$ to the space $X_{n-1}$.

The direct limit over all these skeleta carries the weak topology with respect to all the characteristic maps $\Phi_i^n : D^n \to X_{n}$ which are the extensions of $\phi_i^n$ to the attached inner of the cell. We denote this direct limit by $X$ again.

This is also where you can see "weak topology" and "closure finite", the latter means that a set is closed if its intersection with all skeleta is closed, a property of the direct limit topology.

To avoid some confusion: Such a space $X$ is just a topological space of CW type (= admits a CW structure), whereas the collection of all the skeleta and attaching maps are the CW structure that turns $X$ into a CW complex. There can be different CW structures on the same space, for example the n-sphere can be built from a 0-cell (basepoint) and an n-cell, but one can also introduce intermediate cells from any intermediate sphere.

Some examples where you should be able to come up with CW structures: Tori (possible with a 0-cell, two 1-cells and a 2-cell), projective space (there the attaching map is more interesting), Grassmannians (the famous Schubert cells can be used).

For homotopy theoretic purposes, one can study spaces which may not admit a CW structure, but are homotopy equivalent to a space of CW type. These spaces are called of CW homotopy type, and a prominent example are all smooth manifolds. It is also good to know that all spaces have the weak homotopy type of a CW complex, i.e. every space admits a map to a CW complex such that the map induces isomorphisms on all homotopy groups.

From a CW structure for a space $X$, one can compute the homology and cohomology combinatorically. This is very similar to the Euler identity for planar graphs, that states Edges-Vertices+Faces = Euler-Characteristics (planar graphs are examples of CW complexes).