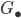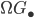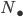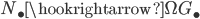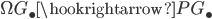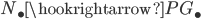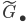This is supposed to be a short intuitive introduction to model categories.

Suppose you have a category $\mathcal{C}$ and some class of morphisms $W$ which behave somewhat like isomorphisms (for example: Chain complexes and Quasi-isomorphisms, or topological spaces and homotopy equivalences, or simplicial sets and weak homotopy equivalences ...). We will call this class "weak equivalences". Then you can look at the localized category $[W^{-1}]\mathcal{C}$, where the morphisms in $W$ are made invertible. If you're lucky, not all objects are isomorphic to each other, and if you're really lucky, you can compute something.

But, as it turns out, usually you don't work with the localized category abstractly, but by some explicit construction of some special case (say, Verdier localization of triangulated categories in the homological setting or explicit homotopies in the topological setting).

Model categories (and its cousins, weak factorization systems, categories of (co)fibrant objects, homotopical categories, etc.) provide a framework to compute stuff in $[W^{-1}]\mathcal{C}$.

[UPDATE 2013-03-06] I gave a 30-Minute talk about model categories, with very little content. [/UPDATE]

Continue reading «Model categories»

In this short posting, I want to give some intuitive idea on homotopy limits. Homotopy (co)limits appear whenever one has a notion of homotopy equivalence or weak equivalence between objects and one doesn't want to have constructions that distinguish between equivalent objects. The most prominent settings are, of course, classical homotopy theory and homological algebra. Although not necessary for the definition of homotopy (co)limits, I also talk about model categories.

Continue reading «Homotopy limits»

Last week Matthias Wendt and I have put our first joint paper on the arXiv, it's called "A¹-fundamental groups of isotropic reductive groups" and here I will tell you how you can think about it without going through all definitions.

I have blogged about this before, but until a few days ago, there was only my diploma thesis in german and an extended abstract in english online, and the results were not as general (oh, and the proofs were also not the best...).

Continue reading «A¹-fundamental groups of isotropic groups»

Every simplicial set admits a universal covering space. If the simplicial set is a simplicial group, the covering can be given a group structure, such that the covering map is a group homomorphism. This can be done "at once" without using geometric realizations, just by close analysis of the usual construction of the universal covering.

Let $G_\bullet$ be a simplicial group, $PG_\bullet$ its path space, $\Omega G_\bullet$ its loop space and $N_\bullet$ the kernel of the projection $\Omega G_\bullet \rightarrow \pi_1(G_\bullet, id)$, which consists of all contractible loops. The composition of $N_\bullet \hookrightarrow \Omega G_\bullet$ with the inclusion $\Omega G_\bullet \hookrightarrow PG_\bullet$ yields a monomorphism $N_\bullet \hookrightarrow PG_\bullet$ whose cokernel we denote by $\tilde{G}_\bullet$.

I claim that this simplicial group already does the job.
Continue reading «Universal coverings of simplicial groups»

I want to discuss the elementary basics of Thom spaces of vector bundles. To start, I explain general one-point compactification and a different construction on vector spaces, then I do it for vector bundles to define the Thom space. I also discuss suspension of topological spaces and how adding a trivial vector space (or bundle) corresponds to suspension under the forming of Thom spaces.

Motto: (Thom space:Suspension)::(Vector bundle:Trivial bundle) or

"Thom spaces are twisted suspensions"

Honestly, I really want to talk about algebraic (motivic) Thom spaces some day, but these are some preliminaries to understand what's going on, so I want to get this out first.

Continue reading «Thom spaces»

These days I read Akhil Mathew's post on Vaserstein's proof of the Quillen-Suslin theorem, once known as Serre's Problem. This inspired the following.

Serre asked whether algebraic vector bundles over affine space are all trivial or not. Quillen and Suslin proved independently that they are, in fact, all trivial. This is some kind of analogue to the topological situation, where all vector bundles over n-dimensional complex affine space (or even n-dimensional real affine space) are trivial.

Continue reading «Is it possible to prove Serre's Problem (the Quillen-Suslin theorem) via Motivic Homotopy ...»