Model categories
Monday, November 12th, 2012 | Author: Konrad Voelkel
This is supposed to be a short intuitive introduction to model categories.
Suppose you have a category  and some class of morphisms
and some class of morphisms  which behave somewhat like isomorphisms (for example: Chain complexes and Quasi-isomorphisms, or topological spaces and homotopy equivalences, or simplicial sets and weak homotopy equivalences ...). We will call this class "weak equivalences". Then you can look at the localized category
which behave somewhat like isomorphisms (for example: Chain complexes and Quasi-isomorphisms, or topological spaces and homotopy equivalences, or simplicial sets and weak homotopy equivalences ...). We will call this class "weak equivalences". Then you can look at the localized category ![[W^{-1}]\mathcal{C}](https://www.konradvoelkel.com/wp-content/plugins/latex/cache/tex_ae2aadcffa93ebb0d0ee28d4f2ff9c57.gif) , where the morphisms in
, where the morphisms in  are made invertible. If you're lucky, not all objects are isomorphic to each other, and if you're really lucky, you can compute something.
are made invertible. If you're lucky, not all objects are isomorphic to each other, and if you're really lucky, you can compute something.
But, as it turns out, usually you don't work with the localized category abstractly, but by some explicit construction of some special case (say, Verdier localization of triangulated categories in the homological setting or explicit homotopies in the topological setting).
Model categories (and its cousins, weak factorization systems, categories of (co)fibrant objects, homotopical categories, etc.) provide a framework to compute stuff in ![[W^{-1}]\mathcal{C}](https://www.konradvoelkel.com/wp-content/plugins/latex/cache/tex_ae2aadcffa93ebb0d0ee28d4f2ff9c57.gif) .
.
[UPDATE 2013-03-06] I gave a 30-Minute talk about model categories, with very little content. [/UPDATE]
A model category is, by definition, a category that is complete and co-complete (which means all limits and colimits over small diagrams exist) and carries a fixed model structure. I will soon explain what that is, but for now I just tell you that a model structure has a class of weak equivalences, too.
The standard procedure to say something about ![\mathcal{C} \to [W^{-1}]\mathcal{C}](https://www.konradvoelkel.com/wp-content/plugins/latex/cache/tex_d33154340ea5627a7d8557472cdb0a84.gif) is to show that
is to show that  is complete and co-complete (if necessary, enlarge
is complete and co-complete (if necessary, enlarge  to a presheaf or sheaf category to get these properties) and endow
to a presheaf or sheaf category to get these properties) and endow  with a model structure that incorporates the class
with a model structure that incorporates the class  as weak equivalences. Then the model structure allows to compute stuff from
as weak equivalences. Then the model structure allows to compute stuff from ![[W^{-1}]\mathcal{C}](https://www.konradvoelkel.com/wp-content/plugins/latex/cache/tex_ae2aadcffa93ebb0d0ee28d4f2ff9c57.gif) in
in  via replacing objects and morphisms by more convenient ones in the same class in
via replacing objects and morphisms by more convenient ones in the same class in ![[W^{-1}]\mathcal{C}](https://www.konradvoelkel.com/wp-content/plugins/latex/cache/tex_ae2aadcffa93ebb0d0ee28d4f2ff9c57.gif) . These replacements are similar to injective/projective resolutions you might know from homological algebra, and they're similar to cellular approximation you might know from topology. Also, mapping cones have their place in the theory.
. These replacements are similar to injective/projective resolutions you might know from homological algebra, and they're similar to cellular approximation you might know from topology. Also, mapping cones have their place in the theory.
In some sense, a model category behaves to ![[W^{-1}]\mathcal{C}](https://www.konradvoelkel.com/wp-content/plugins/latex/cache/tex_ae2aadcffa93ebb0d0ee28d4f2ff9c57.gif) as a group presentation to a group. It is not unique, but useful to calculate. The infinity-category crowd apparently loves this way of thinking.
as a group presentation to a group. It is not unique, but useful to calculate. The infinity-category crowd apparently loves this way of thinking.
Now to the definition of model structures, where I follow the modern axioms of a "closed Quillen model category". I will explain each axiom afterwards.
Definition
A category  together with three classes of morphisms
together with three classes of morphisms 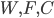 is called a model category if the following axioms are satisfied:
is called a model category if the following axioms are satisfied:
- M1: the category is complete and co-complete.
- M2: the class W satisfies 2-out-of-3.
- M3: retracts of morphisms in
 (resp.
(resp.  ) are again in
) are again in  (resp.
(resp.  ).
). - M4: morphisms in
 satisfy the right lifting property w.r.t.
satisfy the right lifting property w.r.t. 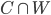
and morphisms in satisfy the left lifting property w.r.t.
satisfy the left lifting property w.r.t.  .
. - M5: there are two functorial factorizations of morphisms into a morphism in
 followed by one in
followed by one in  . In the first, the
. In the first, the  -morphism is also in
-morphism is also in  , in the second, the
, in the second, the  -morphism is also in
-morphism is also in  .
.
The morphisms in  are called weak equivalences, the morphisms in
are called weak equivalences, the morphisms in  are called fibrations, the morphisms in
are called fibrations, the morphisms in  are called cofibrations.
are called cofibrations.
There is one important terminology I have to tell you at this point: an object  is called fibrant if the terminal morphism
is called fibrant if the terminal morphism  is a fibration. An object
is a fibration. An object  is called cofibrant if the initial morphism
is called cofibrant if the initial morphism 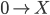 is a cofibration. The initial and terminal morphisms exist because the category is complete and co-complete. From the functorial factorization you get two functors that replace each object by a fibrant (resp. cofibrant) one, and you get a morphism of functors from the identity to each of these functors, which consist of weak equivalences. These are called fibrant and cofibrant replacements.
is a cofibration. The initial and terminal morphisms exist because the category is complete and co-complete. From the functorial factorization you get two functors that replace each object by a fibrant (resp. cofibrant) one, and you get a morphism of functors from the identity to each of these functors, which consist of weak equivalences. These are called fibrant and cofibrant replacements.
We already talked about axiom M1, it essentially means, for every index set, that products and coproducts indexed over this set exist, and that equalizers and co-equalizers indexed over this set exist (together these give all small limits and colimits).
Axiom M2 means, for 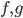 morphisms such that
morphisms such that 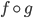 exists, if two out of
exists, if two out of 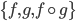 are in
are in  , then all three are in
, then all three are in  . It follows that
. It follows that  is a subcategory, i.e. closed under composition, but M2 is stronger than that.
is a subcategory, i.e. closed under composition, but M2 is stronger than that.
Retracts are to be considered in the arrow category. First, let me remind you of retracts in any category: A morphism  exhibits
exhibits  as a retract if there is a morphism
as a retract if there is a morphism 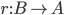 which is a retraction, i.e.
which is a retraction, i.e.  . If we apply this to the arrow category, this means that a morphism
. If we apply this to the arrow category, this means that a morphism  is a retract of
is a retract of 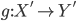 if there are morphisms
if there are morphisms 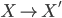 and
and 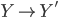 that commute with
that commute with 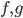 and furthermore exhibit
and furthermore exhibit  and
and  as retracts.
as retracts.
The lifting properties amount to the following: suppose you have a commutative square with  at the left column,
at the left column,  at the right column, anything as rows. Suppose furthermore that
at the right column, anything as rows. Suppose furthermore that  is a cofibration and
is a cofibration and  a fibration. The axioms says, if either
a fibration. The axioms says, if either  or
or  is, in addition, a weak equivalence, then there exists a "lift" in the diagram, that is a morphism from the lower left corner to the upper right corner that commutes with the other four morphisms in the diagram.
is, in addition, a weak equivalence, then there exists a "lift" in the diagram, that is a morphism from the lower left corner to the upper right corner that commutes with the other four morphisms in the diagram.
It follows from this axiom that  are also subcategories, i.e. closed under composition.
are also subcategories, i.e. closed under composition.
Axiom M5 merely states that there are functorial factorizations. In earlier versions of these axioms, people didn't impose functoriality, but nowadays one has it and wants it anyway. Functoriality means functoriality on the arrow category, i.e. if you have a commutative square, you can factorize rows or columns simultaneously and get two new commutative squares inside the original one.
Example
I already promised (somehow) the most important examples. A list of my favourite examples of categories which admit (usually several interesting) model structures:
- Topological spaces
- Simplicial sets
- Chain complexes over an Abelian category
- Functor categories over a model category
- Simplicial (pre)sheaves over a Grothendieck site
There are very strong connections between these model categories (oh, I should really say: the various model structures on each of these categories are tightly connected and there are similar connections between particular model structures on different categories). The technical term is Quillen equivalence.
Instead of repeating more textbook knowledge (which is better written elsewhere) I just give you a sketch of the proof that one can endow topological spaces with a sensible model structure:
Let us take W = homotopy equivalences, F = Hurewicz fibrations and C = all maps that satisfy a right lifting property w.r.t. Hurewicz fibrations that are homotopy equivalences. Hurewicz fibrations are themselves defined by a lifting property: they have the left lifting property w.r.t. all maps ![X \to X \times [0,1]](https://www.konradvoelkel.com/wp-content/plugins/latex/cache/tex_a3713715d62bb67923eead359b7cbf0e.gif) that embed
that embed  as
as  .
.
M1 is done by hand, i.e. construct limits and colimits by writing down sets and topologies that satisfy the universal properties.
M2 and M3 is done by using homotopy inverses.
M4 can be shown by a "small object argument" which I won't explain here. If you think for a moment how you would prove it, you will almost immediately have an almost solution, where only the "small object argument" is missing.
M5 is done by the familiar mapping cylinder and mapping path space constructions.
Next reading
If you read this, you're probably new to the model category business. Some helpful articles are to be found on Daniel Dugger's homepage. I also liked Dwyer & Spalinski's introduction. There is no way around the textbooks of Hovey and Hirschhorn. Perhaps a good place to go first would be May's Concise Course in Algebraic Topology, because it secretly introduces the reader to thinking model-categorically. The next step could then be Goerss & Jardine's Simplicial Homotopy Theory.
2012-11-17 (17. November 2012)
For someone who is familiar with derived categories but unfamiliar with most of model category theory, I have wondered about the following question:
Are there "quick" examples of how model category theory aids in understanding for instance the derived category of the homotopy category of chain complexes, where the set W is the set of quasiisomorphisms? For instance, what are some computations/proofs that become clearer with the aid of model categories?
2012-11-17 (17. November 2012)
Something that comes to my mind are mapping cones. See for example http://mathoverflow.net/questions/111941/good-morphisms-of-distinguished-triangles-can-neemans-method-be-applied-to-the
but I could probably say something more .. as soon as I have time :-)