Haar measure in different settings
Sunday, November 15th, 2009 | Author: Konrad Voelkel
I recently learned how to build a Haar measure on every locally compact group. It's a fact there is only one (up to positive scalar multiple) Haar measure on a locally compact group, and it's easy to see that Lie groups (which includes algebraic and finite groups) and all compact groups are locally compact, so they have a unique (up to scalar multiple) Haar measure, too.
But the Haar measure can be defined much easier for Lie groups, and it's even simpler for finite groups. I wanted to study the relation more directly than by the uniqueness proof one sees in the literature.
This text is intended to be read by anyone who is familiar with the notion of groups and measures. Maybe you will want to consult Wikipedia along the lines - I have included some links.
I give first a precise definition of Haar measure and a state its uniqueness on locally compact groups, then I compare the different types of topological groups I want to investigate, along with valid definitions of Haar measure.
Definition of Haar measure; Uniqueness
Recall that a (left) Haar measure on a topological group  is a (left-)translation invariant measure
is a (left-)translation invariant measure 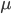 that is finite on compact sets and not everywhere zero.
that is finite on compact sets and not everywhere zero.
(Left-)Translation invariance means, that for all sets 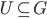 and elements
and elements 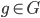 we have
we have  . This can of course be defined from the right side, too, but the left and the right Haar measure are not the same, in general. Groups whose left and right Haar measure coincide are called unimodular. Abelian locally compact groups are always unimodular.
. This can of course be defined from the right side, too, but the left and the right Haar measure are not the same, in general. Groups whose left and right Haar measure coincide are called unimodular. Abelian locally compact groups are always unimodular.
A Haar measure is called normalized if it has total measure 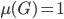 .
.
Theorem: If there are two Haar measures  on a topological group
on a topological group  , then
, then  for some positive real constant
for some positive real constant 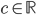 .
.
This can be proved by fuddling around with double integrals and using left translation invariance multiple times, see the literature referenced at the bottom of this post.
Comparision chart of groups I discuss
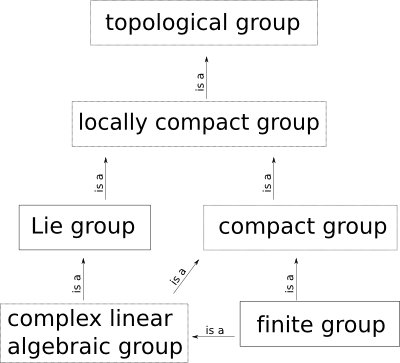
The case of arbitrary topological groups is discussed quickly: the example of infinite dimensional Banach space, which is not locally compact, and admits no Haar measure (which would be infinite Lebesgue measure).
Haar measure on a locally compact group
The basic idea is to define a left-translation-invariant content which will then yield, by standard measure theory, the Haar measure. This proof uses Tychonoff's theorem and therefore the Axiom of Choice. There exists a proof which doesn't use Axiom of Choice but it requires more analysis (the Kakutani fixed point theorem or some functional analysis) and can be found in the literature.
Take  a nonempty compact subset of the group and
a nonempty compact subset of the group and  a subset with nonempty interior (so
a subset with nonempty interior (so  contains some nonempty open set). Denote by
contains some nonempty open set). Denote by  the minimal
the minimal  such that there exists
such that there exists  with
with 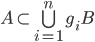 . The number
. The number  is always finite because of
is always finite because of  's compactness. Denote by
's compactness. Denote by  the set of all neighbourhoods of the identity of
the set of all neighbourhoods of the identity of  . For some
. For some  , define for compact sets
, define for compact sets  :
:

Then we have
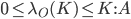 .
.This
 is almost a content, but it lacks additivity.
is almost a content, but it lacks additivity.
For each compact set 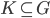 define the interval
define the interval ![I_K := [0, K : A]](https://www.konradvoelkel.com/wp-content/plugins/latex/cache/tex_f0481df37665f94570387a85ccb4ff34.gif) .
.
Now define the infinite product  , which is compact by Tychonoff's theorem. The elements of
, which is compact by Tychonoff's theorem. The elements of 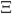 are functions
are functions  that assign each compact set
that assign each compact set  a non-negative value below
a non-negative value below 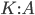 . Our previously defined
. Our previously defined  are elements of
are elements of 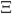 for all
for all  .
.
Look at
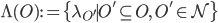
for some
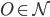 . For some family
. For some family 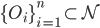 , we have
, we have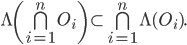
where the left hand side is nonempty, therefore is the right hand side nonempty. Compactness of
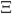 tells us now that there exists some point in the intersection of the closures of the
tells us now that there exists some point in the intersection of the closures of the  :
: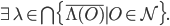
And I claim that this
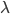 is the left-invariant content we're looking for. Again, for the full proof I refer to the literature.
is the left-invariant content we're looking for. Again, for the full proof I refer to the literature.
Haar measure on a compact group
Compact groups are all unimodular:
Define the modulus to be 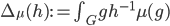 . Then
. Then  is unimodular iff
is unimodular iff  . For a compact group
. For a compact group  , the continuous group homomorphism
, the continuous group homomorphism 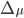 has values in the additive group
has values in the additive group  , whose only compact subgroup is
, whose only compact subgroup is  .
.
More directly, one could, in analogy to finite groups, do this:
Take a left Haar measure 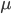 and some open set
and some open set 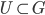 . Then, via compactness, there is a family
. Then, via compactness, there is a family  such that
such that  . Define a measure
. Define a measure  . This is clearly right-invariant and it's not hard to see that it coincides with
. This is clearly right-invariant and it's not hard to see that it coincides with 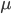 . The hard part is to check that
. The hard part is to check that  is a well-defined measure.
is a well-defined measure.
One can prove existence of a Haar measure on a compact group with less effort than for an arbitrary locally compact group. A nice fact is, that there always exists a normalized Haar measure, since the volume of a compactum is finite and  defines a normalized Haar measure for every Haar measure
defines a normalized Haar measure for every Haar measure 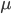 .
.
Haar measure on a Lie group
Lie groups are differential manifolds, so there is a top outer form  for
for 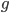 the Lie algebra of
the Lie algebra of  (the tangent space at the identity element;
(the tangent space at the identity element; 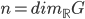 ). You might call this form a scalar multiple of the determinant, since it's exactly that for the Lie groups
). You might call this form a scalar multiple of the determinant, since it's exactly that for the Lie groups 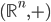 . The determinant form can be integrated and this is the Haar measure for Lie groups.
. The determinant form can be integrated and this is the Haar measure for Lie groups.
The special case of 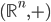 is just the Lebesgue measure.
is just the Lebesgue measure.
The special case of 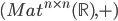 is the Lebesgue measure divided by the absolute value of the determinant, so
is the Lebesgue measure divided by the absolute value of the determinant, so 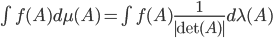 with
with 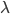 being the Lebesgue measure in
being the Lebesgue measure in  .
.
Haar measure on a linear complex algebraic group
Linear complex algebraic groups are compact Lie groups, so the Haar measure is given explicitely by a differential form, it's unimodular and there is always a normalized Haar measure.
I included this case only to show how nice it behaves - almost like finite groups.
Of course, finite groups are linear complex algebraic groups, since finite sets are just a finite number of copies of  , and linearity is no condition in this case. There are no chart intersections, thus no chart transformation condition has to be satisfied. But I think this is a rather counter-intuitive way to think of finite groups, and it's still amazing to see how many properties all linear complex algebraic groups share with them.
, and linearity is no condition in this case. There are no chart intersections, thus no chart transformation condition has to be satisfied. But I think this is a rather counter-intuitive way to think of finite groups, and it's still amazing to see how many properties all linear complex algebraic groups share with them.
Haar measure on a finite group
Here we can just give every group element the weight  , since
, since  is finite. The formula
is finite. The formula 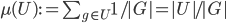 for every subset
for every subset 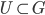 defines a Haar measure.
defines a Haar measure.
The number 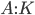 for locally compact groups, defined above, corresponds to the smallest integer greater than
for locally compact groups, defined above, corresponds to the smallest integer greater than 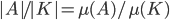 . Now one might understand the proof above a little bit better.
. Now one might understand the proof above a little bit better.
The "why"
So, whenever we have a formula for finite groups, where some averaging over the group is done, we can try to lift this formula to compact groups, Lie groups or even locally compact groups, using the integral instead the sum. One particular application is the definition of a translation-invariant hermitian form on the class functions, which is very useful in representation theory.
References
- Simon Rubinstein-Salzedo : "On the Existence and Uniqueness of Invariant Measures on Locally Compact Groups" (2004) (where I have stolen the proof sketch parts in the general case)
- Dieudonné: Treatise on analysis II, where you can find another nice proof of existence & uniqueness of Haar measure on locally compact (sepeable, metrizable) groups. This can be found as DjVu in the 'net, but that requires some searching.

2011-02-24 (24. February 2011)
If the Haar measure of a locally compact abelian group G is
finite, Is the group G compact? thanks!
2011-02-26 (26. February 2011)
I don't know the answer, but here are my wild guesses:
If G would be compact, the Pontryagin dual G^ = Hom(G,T) would be discrete (with the compact-open topology).
If you could show that the Pontryagin dual is discrete, then with Pontryagin duality you get that G is compact.
Discrete topology of G^ means, every one-point set {f} of functions f : G -> T would have to be the finite intersection of sub-basis sets of the compact-open topology: O(K,U) = {phi : G -> T s.t. phi(K) is a subset of U} for K compact in G and U open in T. Alternatively, you could show by some other means that the topology of uniform convergence (which is the same) is discrete.
Also I think it would be nice if you could tell me whether this is your homework or a research question before I try to solve it ;-)