If you don't have a solid education in linear algebraic groups, you might nevertheless encounter the term "reductive groups" now and then. People keep telling you to think about 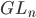$GL_n$, as an algebraic group, and that's a good first approximation. If you want to go a step further, some confusion can happen, since the definition of reductive groups can be given for groups over the complex numbers in two quite different ways and only one of them generalizes to reductive groups over other fields, and if one wants to do non-perfect fields, it gets even more complicated.

I want to give some very short explanations on how to think about reductive groups and semisimple algebraic groups.

Continue reading «What is ... a reductive group?»

I recently learned how to build a Haar measure on every locally compact group. It's a fact there is only one (up to positive scalar multiple) Haar measure on a locally compact group, and it's easy to see that Lie groups (which includes algebraic and finite groups) and all compact groups are locally compact, so they have a unique (up to scalar multiple) Haar measure, too.
But the Haar measure can be defined much easier for Lie groups, and it's even simpler for finite groups. I wanted to study the relation more directly than by the uniqueness proof one sees in the literature.
This text is intended to be read by anyone who is familiar with the notion of groups and measures. Maybe you will want to consult Wikipedia along the lines - I have included some links.

I give first a precise definition of Haar measure and a state its uniqueness on locally compact groups, then I compare the different types of topological groups I want to investigate, along with valid definitions of Haar measure.
Continue reading «Haar measure in different settings»