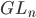Classification of Division Algebras
Tuesday, January 27th, 2015 | Author: Konrad Voelkel

I was asked to give a talk about division algebras (purpose and classification). This is a rough overview of it, mostly learned from the book of Springer and Veldkamp "Octonions, Jordan Algebras and Exceptional Groups" and the book of Lam "Noncommutative Rings". The book "Numbers" by Ebbinghaus et al. was also nice to read along for references.
We will look mostly at finite dimensional (not neccesarily associative) division algebras over the real numbers.
Instead of these rather loose notes, you may prefer to look at my texed notes in this pdf file.
Category: English, Mathematics | Comments off