This post is the continuation of "From the Langlands Correspondence for Function Fields to the Geometric Langlands Correspondence I", and explains how to translate the Langlands Correspondence for function fields to a geometric question.

This post grew out of the preparation for a seminar talk on this topic and is separated in two parts, this being the second, and last part.

To repeat briefly, the Langlands Correspondence for a function field 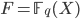$F = \mathbb{F}_q(X)$ of a smooth projective curve $X$ states that certain n-dimensional irreducible l-adic Galois representations correspond (1:1) to irreducible cuspidal automorphic representations of $GL_n(\mathbb{A}_F)$. Furthermore, the L-functions of Galois representations and automorphic representations coincide.

Continue reading «From the Langlands Correspondence for Function Fields to the Geometric Langlands Correspon...»

The (conjectural) Langlands correspondence for number fields gave rise to a Langlands correspondence for function fields (proved by Drinfeld and Lafforgue), where the most important difference is the absence of the infinite place which simplifies things in the latter. This, in turn, can be translated to a "geometric" Langlands correspondence for curves over fields, but there are certain differences.

First, I'm going to explain what the Langlands correspondence for function fields says, with the assumption in mind that you have been exposed to some algebra before. After that, I'm going to sketch how to go to the geometric Langlands correspondence, following Frenkel's storytelling in chapter 3 of his article "Langlands and conformal field theory". Of course, this being a blogpost, I won't repeat what Frenkel says (nor delve deeper) but try to summarise, to give an overview.

This post grew out of the preparation for a seminar talk on this topic and is separated in two parts, this being the first part. The continuation is here, discussing the geometrization.

Continue reading «From the Langlands Correspondence for Function Fields to the Geometric Langlands Correspon...»