Two connected compact manifolds N and M are said to be bordant, if there exists a manifold W with boundary consisting of two connected components isomorphic to N and M respectively. The name comes from french and means sharing a boundary. Some people say cobordant, since the manifolds don't share a boundary but "are" shared as a boundary (I don't know how to explain this better than with the definition given above). We will stick to "bordant" because we investigate precisely what "the bordism of a manifold" and "the cobordism of a manifold" are.

One can see that being bordant is an equivalence relation, so it makes sense to speak of bordism classes of manifolds. By enriching N and M with extra structure (like a tangential framing, or an orientation), we get several different notions of bordism classes.

From each of these bordism theories, we get a sequence of spaces 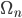$\Omega_n$ such that 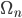$\Omega_n$ is the Thom space of a universal bundle over some classifying space (I will explain that later) and 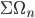$\Sigma \Omega_n$ is homotopy equivalent to $\Omega_{n+1}$. Homotopy theorists like to call such a sequence then a spectrum and by standard theory one can associate to each spectrum a generalized homology theory and a generalized cohomology theory. Even better, Brown's representability theorem states that every generalized (co)homology theory comes from a spectrum, so we have a 1:1 correspondence.

The goal of this article is now to define Thom spectra and to give a geometric interpretation of the corresponding homology and cohomology theories, essentially by carrying out the Pontryagin-Thom construction relatively.

Continue reading «Bordism and Cobordism»

Last week Matthias Wendt and I have put our first joint paper on the arXiv, it's called "A¹-fundamental groups of isotropic reductive groups" and here I will tell you how you can think about it without going through all definitions.

I have blogged about this before, but until a few days ago, there was only my diploma thesis in german and an extended abstract in english online, and the results were not as general (oh, and the proofs were also not the best...).

Continue reading «A¹-fundamental groups of isotropic groups»