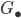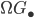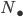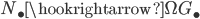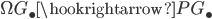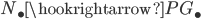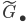All these fundamental groups!
Tuesday, April 02nd, 2013 | Author: Konrad Voelkel

There are a lot of fundamental groups floating around in mathematics. This is an attempt to collect some of the most popular and sketch their relations to each other.
Category: English, Mathematics | Comments off