Bordism and Cobordism
Monday, July 23rd, 2012 | Author: Konrad Voelkel

Two connected compact manifolds N and M are said to be bordant, if there exists a manifold W with boundary consisting of two connected components isomorphic to N and M respectively. The name comes from french and means sharing a boundary. Some people say cobordant, since the manifolds don't share a boundary but "are" shared as a boundary (I don't know how to explain this better than with the definition given above). We will stick to "bordant" because we investigate precisely what "the bordism of a manifold" and "the cobordism of a manifold" are.
One can see that being bordant is an equivalence relation, so it makes sense to speak of bordism classes of manifolds. By enriching N and M with extra structure (like a tangential framing, or an orientation), we get several different notions of bordism classes.
From each of these bordism theories, we get a sequence of spaces 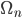 such that
such that 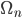 is the Thom space of a universal bundle over some classifying space (I will explain that later) and
is the Thom space of a universal bundle over some classifying space (I will explain that later) and 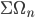 is homotopy equivalent to
is homotopy equivalent to  . Homotopy theorists like to call such a sequence then a
. Homotopy theorists like to call such a sequence then a
The goal of this article is now to define Thom spectra and to give a geometric interpretation of the corresponding homology and cohomology theories, essentially by carrying out the Pontryagin-Thom construction relatively.
Category: English, Mathematics | 2 Comments
