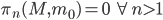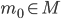Mindmap on complex analysis in one variable
Monday, November 14th, 2011 | Author: Konrad Voelkel

Here is my mind-map for first-course complex analysis. It contains some well-known theorems and "arrows" between them.
Here it is, and of course you can download it as a PDF or as a SVG (vector graphics) as well (click on the image to enlarge it):

The license is CC-BY-NC-SA (if you redistribute, put my name on it, don't make profit, share alike).
There are some aspects which require an explanation:
Continue reading «Mindmap on complex analysis in one variable»
Category: English, Mathematics | Comments off


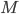

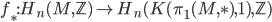
![[M] \in H_n(M,\mathbb{Z})](https://www.konradvoelkel.com/wp-content/plugins/latex/cache/tex_6fd228685037a445f5a86e7d621040ec.gif)
![f_\ast([M]) \neq 0 \in H_n(K(\pi_1(M,\ast),1),\mathbb{Z})](https://www.konradvoelkel.com/wp-content/plugins/latex/cache/tex_625b0d4c3630329950c69a5f6cb9f126.gif)