As I'm currently reading Morel&Voevodskys paper on A¹-homotopy theory of schemes, I will by and by write a little "walk-through" with hints & comments on how to find additional information to better (or even start to) understand the paper. Maybe for a newcomer to the subject (like me) it's difficult at first to stick together all these concepts like model theory, simplicial objects, Grothendieck topologies, algebraic geometry and so on. I will try to provide helpful comments to make the paper more accessible to those who are not that familiar with these notions above.

The paper is available (for free) at NUMDAM: http://www.numdam.org/item?id=PMIHES_1999__90__45_0

And I will begin right now, on page 1 (well, on page 45 in the IHES tome 90):
The author suggests reading some additional sources. I suggest we just continue reading the paper we already started with ;-) But for any introductory notes, I refer to this wonderful paper of Dwyer & Spalinski which makes one comfortable with model categories. For further links, see this page and this blog.

On page 46, the definition of a model category is given. If you don't know what a category is, you should definitely consider MacLane: Categories for the working mathematician (or any other introductory textbook about it, but I learned pretty much from MacLane). In fact, you should stop what you're doing right now and start learning about categories until you really know what limits and colimits are. Then you can continue doing your stuff (and go back to MacLane later). More generalities about model categories can be learned from Hoveys wonderful book.

To get a feeling about model categories, you might try to prove that the category of topological spaces, with Serre fibrations as fibrations and relative CW complexes as cofibrations, together with weak homotopy equivalences as weak equivalences, form a model category (but it's not that easy!). If you don't know what a Serre fibration or a relative CW complex is, you might want to read (parts of) Hatchers book, which is available online for free. (Well, if you don't know this book yet, you should give it a try anyway). If you once knew what this is but don't remember exactly or just want to get a good, clean overview, try Mays "Concise Course in Algebraic Topology" (I love it).

Then there is a small comment about sites, which are taken to have enough points. You can read about sites (Grothendieck topologies) in SGA4, like Voevodsky suggests, but other sources are more easy to read as introduction: Illusie wrote a 'What is ... a topos' article in the AMS notices.

To give you an introduction right here: A pretopology on a category is a way to specify what a cover should be in this category. Every pretopology leads to a Grothendieck topology (which is not so nice to define) and we call a category equiped with a Grothendieck topology a site. The category of sheaves on a site (or some category equivalent to that) is called a topos. You may ask what a sheaf on a site should be - well, just a presheaf on the category which satisfies the sheaf axiom with respect to the Grothendieck topology. To understand the definitions, it's very helpful to rephrase the definition of a sheaf on a topological space in terms of functors and coequalizers, so you can directly see why sheaves on a site are the immediate generalisation.

If you understood this, you might ask yourself: "Ok, but what is a site with enough points?".This means "a site whose category of sheaves on it has enough points", because by definition, a point of a site is a point of the topos of sheaves on it.
Early in the paper (p. 48), Voevodsky reminds us that a point of a topos T is a functor 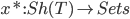$x* : Sh(T) \rightarrow Sets$.

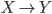What is a point of a topos? By definition just a morphism of the topos $pt$ to the topos in question. A morphism of topoi $X \rightarrow Y$ is a geometric morphism, that is a pair of adjoint functors 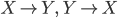$X \rightarrow Y,\ Y \rightarrow X$. The topos $pt$ is the category of sets (well, sheaves of sets on the topological space which consists of a single point, if you want proof that it's really a topos).

So a point of a topos X is a pair of adjoint functors 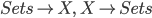$Sets \rightarrow X,\ X \rightarrow Sets$. We should think of this as "selecting a point of X" and the corresponding stalk functor. For more detail, have a look at the great n-category n-lab wiki article about points of topoi or (even more detail) at MacLanes and Moerdijks book on Topoi (this is where I learned my topos theory from - and you can get a scanned DjVu version somewhere in the web, too).

If we construct a topos from a topological space, each classic point gives us a topos-theoretic point. Strangely, there are topoi without points (there are just no pairs of adjoint functors at all). So, if we want to talk about points, we need a notion of topoi with enough points. For us, it will be sufficient to think about this property of being "all isomorphisms can be tested stalk-wise", which is certainly a useful property of sheaves on topological spaces.

By the way, it should be said that many SGA and EGA are available online, most as scanned DjVu files but some (SGA4, for example) TeXed, so you can use a full-text-search engine in your PDF reader. You can find most recent hyperlinks on the Wikipedia page about re-published SGAs.

On the next page (47), simplicial sheaves are discussed. The book cited [22], Mays "simplicial objects in algebraic topology" is very nice to read (and available as DjVu ... if you search a little bit), so I recommend having a glimpse on, say, the first two chapters. It is easy and fun to read if you always try to translate each theorem/proof in geometry.

Enough for today. Next time I will talk more about the content of the paper than giving links to other sources... Of course, if you have suggestions what I should explain less or further, or find any mistakes, please write a comment about it!