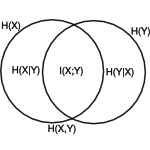
Some thoughts on AQFT (algebraic or axiomatic quantum field theory)
Monday, August 08th, 2011 | Author: Konrad Voelkel

In this post, I want to explain briefly the idea behind AQFT in the Haag-Kastler style. To motivate this, let me first sketch what QFT (= quantum field theory) is about, at least in my mathematically distorted perception.
Classical quantum theory is about modelling purely quantum effects, i.e. without considering gravity, or at least without considering relativistic effects. There, a separable Hilbert space as a state space is appropriate. The bounded linear operators on the state space form a certain kind of normed algebra with compatible involution (taking the adjoint) called C*-algebra and measurements correspond to self-adjoint operators.
Quantum field theory tries to incorporate quantum mechanics into electromagnetic field theory (or vice versa) and gravitational field theory. So far, no such theory-of-everything has been developed with falsifiable predictions, although there are some promising candidates.
Continue reading «Some thoughts on AQFT (algebraic or axiomatic quantum field theory)»
Category: English | Comments off