Every simplicial set admits a universal covering space. If the simplicial set is a simplicial group, the covering can be given a group structure, such that the covering map is a group homomorphism. This can be done "at once" without using geometric realizations, just by close analysis of the usual construction of the universal covering.

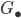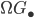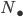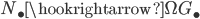Let $G_\bullet$ be a simplicial group, $PG_\bullet$ its path space, $\Omega G_\bullet$ its loop space and $N_\bullet$ the kernel of the projection $\Omega G_\bullet \rightarrow \pi_1(G_\bullet, id)$, which consists of all contractible loops. The composition of $N_\bullet \hookrightarrow \Omega G_\bullet$ with the inclusion 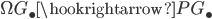$\Omega G_\bullet \hookrightarrow PG_\bullet$ yields a monomorphism 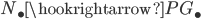$N_\bullet \hookrightarrow PG_\bullet$ whose cokernel we denote by $\tilde{G}_\bullet$.

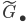I claim that this simplicial group already does the job.
Continue reading «Universal coverings of simplicial groups»