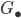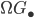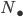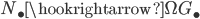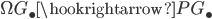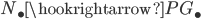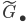This is a very short notice to memorize some of the various model structures on simplicial presheaves in a systematic way.

[UPDATE 2013-03-06] I gave a talk in our working group seminar about model structures on simplicial presheaves, homotopy sheaves and h-principles [/UPDATE]

Continue reading «Model structures on simplicial presheaves»

Last week Matthias Wendt and I have put our first joint paper on the arXiv, it's called "A¹-fundamental groups of isotropic reductive groups" and here I will tell you how you can think about it without going through all definitions.

I have blogged about this before, but until a few days ago, there was only my diploma thesis in german and an extended abstract in english online, and the results were not as general (oh, and the proofs were also not the best...).

Continue reading «A¹-fundamental groups of isotropic groups»

Every simplicial set admits a universal covering space. If the simplicial set is a simplicial group, the covering can be given a group structure, such that the covering map is a group homomorphism. This can be done "at once" without using geometric realizations, just by close analysis of the usual construction of the universal covering.

Let $G_\bullet$ be a simplicial group, $PG_\bullet$ its path space, $\Omega G_\bullet$ its loop space and $N_\bullet$ the kernel of the projection $\Omega G_\bullet \rightarrow \pi_1(G_\bullet, id)$, which consists of all contractible loops. The composition of $N_\bullet \hookrightarrow \Omega G_\bullet$ with the inclusion $\Omega G_\bullet \hookrightarrow PG_\bullet$ yields a monomorphism $N_\bullet \hookrightarrow PG_\bullet$ whose cokernel we denote by $\tilde{G}_\bullet$.

I claim that this simplicial group already does the job.
Continue reading «Universal coverings of simplicial groups»

We look at the model structure Voevodsky and Morel use in their 1999 IHES paper and discuss 1.2, 1.3, 1.4, 1.5, 1.6, 1.8, 1.9, 1.10. There is nothing difficult or particularly interesting, but you might want to look up some specific issue or reference.
Continue reading «Walk-through to Morel-Voevodsky A¹-homotopy theory, page 48-50»