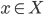A vector bundle is a morphism that looks locally on the target like a product of the target with a vector space.

We will call the target space the base and the space of definition the total space. The preimage of a point of the base is called the fiber.

Is that the correct mathematical definition? It doesn't mention what kind of spaces we look at, what kind of morphism I'm talking about, what the product is, locally in which sense, vector space over which field, do we allow infinite dimension, ... so it's not a mathematical definition in the pedantic sense. I will give you pedantic definitions in this article, just to satisfy my need to write down what I consider to be a good terminology.

Continue reading «What is ... a vector bundle?»

Nowadays it is common to use $x \mapsto f(x)$ to denote that an element $x \in X$ is mapped to an element $f(x) \in Y$ by the map(ping) $f : X \to Y$. In particular, the arrow $\rightarrow$ (in LaTeX: \rightarrow) denotes a map, or more generally a morphism, while $\mapsto$ (in LaTeX: \mapsto) denotes how particular elements or objects are mapped to other elements or objects.

Have you ever seen an arrow which has a triangle as head? Like those:

Continue reading «An arrow notation for annotations»