
Kürzlich habe ich mal versucht NichtmathematikerInnen zu erklären, was ich da eigentlich so mache (in meinem Mathematikstudium).
Da ich algebraische Geometrie benutze, wollte ich versuchen die Intuition zu vermitteln, was ein Schema ist oder wieso man in diese Richtung denkt. Das versuche ich jetzt also einmal in geschriebener Form:
Stell dir einen Kreis mit Radius  vor, also die Menge aller Punkte, die vom Mittelpunkt des Kreises genau den Abstand
vor, also die Menge aller Punkte, die vom Mittelpunkt des Kreises genau den Abstand  haben. In der
haben. In der  -Ebene lässt sich ein Kreis, dessen Mittelpunkt der Ursprung
-Ebene lässt sich ein Kreis, dessen Mittelpunkt der Ursprung  ist, leicht beschreiben, denn der Abstand vom Nullpunkt ist für einen Punkt
ist, leicht beschreiben, denn der Abstand vom Nullpunkt ist für einen Punkt  gegeben durch die Formel
gegeben durch die Formel  . Der Kreis wird dann beschrieben durch die Menge
. Der Kreis wird dann beschrieben durch die Menge  , dabei bedeutet
, dabei bedeutet  ganz einfach, dass
ganz einfach, dass  ein Punkt in der Ebene ist, dessen Koordinaten
ein Punkt in der Ebene ist, dessen Koordinaten  und
und  reelle Zahlen sind, also z.B.
reelle Zahlen sind, also z.B.  oder auch
oder auch  usw. Jetzt schreibe ich die Menge
usw. Jetzt schreibe ich die Menge  noch ein kleines bisschen anders:
noch ein kleines bisschen anders:
 , man überzeuge sich davon, dass dies die selbe Menge von Punkten in der Ebene
, man überzeuge sich davon, dass dies die selbe Menge von Punkten in der Ebene  ist.
ist.
Continue reading «Mathe für Nichtmathematiker»

 zwischen Riemannschen Flächen
zwischen Riemannschen Flächen 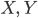 , können wir uns fragen: Ist
, können wir uns fragen: Ist  eine Überlagerung? Unter welchen hinreichenden oder notwendigen Bedingungen?
eine Überlagerung? Unter welchen hinreichenden oder notwendigen Bedingungen?






























