Lagrange and the Supernaturals
Friday, August 03rd, 2012 | Author: Konrad Voelkel
You might know the theorem of Lagrange from group theory: A finite group of order n can have a subgroup of order m only if m divides n. Here the order is just the number of elements, a natural number.
Recently I came across a generalization to profinite groups. How do you make sense of the order of an infinite group? How to say that the order of a subgroup divides the order of the group? The solution is a simple concept called supernatural numbers, which I will explain in this short article. The main part should in principle be accessible to non-mathematicians as well.
Any natural number n which is not zero has a unique prime factorization

where the exponents
 are natural numbers, including possibly zero, and all but finitely many exponents are zero.
are natural numbers, including possibly zero, and all but finitely many exponents are zero.
We can thus identify each natural number (except 0) with a list of natural numbers, the first entry being the exponent 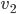 of the first prime 2, the second entry being the exponent
of the first prime 2, the second entry being the exponent  of the second prime 3, and so on. I draw a picture in my head, where these lists are written on infinite sheets of paper, each natural number corresponds to one such sheet of paper.
of the second prime 3, and so on. I draw a picture in my head, where these lists are written on infinite sheets of paper, each natural number corresponds to one such sheet of paper.
Now we generalize this, by allowing the exponent  for any prime, i.e. we allow sheets of paper where on the list some of the entries are no longer natural numbers but may be the new symbol
for any prime, i.e. we allow sheets of paper where on the list some of the entries are no longer natural numbers but may be the new symbol  . We also allow arbitrarily many of the entries to be non-zero.
. We also allow arbitrarily many of the entries to be non-zero.
This has no meaning so far, but we will give it some meaning. I will call the new collection of lists the supernaturals. Some people prefer other terms, such as Steinitz numbers (for the inventor Ernst Steinitz) or the boring and possibly confusing term "generalized natural numbers".
If one natural number 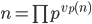 is multiplied with another natural number
is multiplied with another natural number 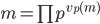 , the product has the prime factorization
, the product has the prime factorization
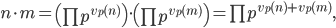
so multiplication of natural numbers corresponds to adding the numbers on the list of exponents.
We can define a "multiplication" on the supernatural numbers by defining the "product" of two lists of exponents to be the list of sums of exponents (as we have just seen). In case we have to add
 for some natural number k, we define this to be
for some natural number k, we define this to be  again. If we have to add
again. If we have to add 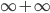 , we define this to be
, we define this to be  again as well.
again as well.
If one natural number n divides another one m, this just means there is some natural number k such that  , so we can express this in terms of the exponents: n divides m if the exponents in the prime factorization of n are all smaller or equal than the exponents of m in the prime factorization.
, so we can express this in terms of the exponents: n divides m if the exponents in the prime factorization of n are all smaller or equal than the exponents of m in the prime factorization.
In other words: n divides m if and only if all entries on the list of exponents are smaller or equal than those of m. This definition can be used for supernaturals: a supernatural number x is defined to divide another supernatural number y if all entries of x are (entry-wise) smaller or equal than y. Entry-wise means that the first entry should be smaller or equal to the first, while the second entry should be smaller or equal to the second, and so on.
This is exactly the same as requiring that there is a third supernatural number z such that  , with the multiplication of supernatural defined above.
, with the multiplication of supernatural defined above.
There is no such thing as adding two supernatural numbers, because adding two natural numbers can not be expressed in terms of the prime factorization; but that shouldn't keep us from calling them numbers.
A mathematician would write a supernatural number not in the form of an infinite list, but rather use the suggestive notation

with
 , without any further restrictions.
, without any further restrictions.Here you have to be careful: The product sign doesn't really mean "product" in any sense other than the multiplication of supernatural numbers, so if you take the notation as definition, the symbol
 is just a formal symbol, without any "meaning".
is just a formal symbol, without any "meaning".
The promised generalization of Lagrange's theorem is: A profinite group of order x can have a subgroup of order y only if y divides x -- where x and y are supernatural numbers.
I will now explain how to define the order of a profinite group as a supernatural number, but for that I have to take limits in the supernatural numbers.
Remember in the natural numbers, if you take a sequence of growing numbers, like

they become infinitely large and hence we write
 (even if
(even if  is not a natural number).
is not a natural number).We have to be more careful now. If you take the sequence
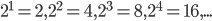
we want the limit to be
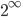 .
.
In general, we want to compute limits entry-wise on the list of exponents. The sequence  corresponds to the sequence of lists which start with
corresponds to the sequence of lists which start with 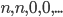 and then only zeroes (since that is the list of exponents for the number
and then only zeroes (since that is the list of exponents for the number 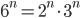 ). The limit of
). The limit of  is therefore the supernatural number with entries
is therefore the supernatural number with entries  and then only zeroes (since we defined it that way). To be concrete,
and then only zeroes (since we defined it that way). To be concrete,  and thus
and thus  .
.
You might have noticed that we don't actually allow a thing like  to be a supernatural number itself. Instead, there are various "infinitely large" supernatural numbers, like
to be a supernatural number itself. Instead, there are various "infinitely large" supernatural numbers, like  , which are all different. It is a subtle point to remark that
, which are all different. It is a subtle point to remark that  , since
, since 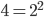 , so
, so  , but you don't need to understand that right now.
, but you don't need to understand that right now.
If you really want to use the symbol  for a supernatural number, it should probably be the limit of the sequence
for a supernatural number, it should probably be the limit of the sequence  , i.e.
, i.e. 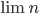 . It is a good exercise to figure out how the supernatural limit looks like and what the divisors of this number are!
. It is a good exercise to figure out how the supernatural limit looks like and what the divisors of this number are!
Any profinite group can be written as (inverse) limit over finite groups (hence the name), and these finite groups have an order (the number of elements). Taking the limit over these orders, in the supernatural sense, gives a supernatural number which we call the order of the profinite group.
A basic example is 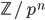 , which is of order
, which is of order  , and the inverse system
, and the inverse system 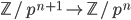 has a limit group written
has a limit group written  , the p-adic integers. They have order
, the p-adic integers. They have order  , a supernatural number. The only (supernatural) numbers that divide
, a supernatural number. The only (supernatural) numbers that divide  are all
are all  and Lagrange tells us that these are exactly the orders of subgroups you get. I tell you that these are exactly the subgroups
and Lagrange tells us that these are exactly the orders of subgroups you get. I tell you that these are exactly the subgroups 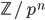 .
.
I think the supernaturals are a super-cute example of mathematics that can be explained in school. The application to group theory can be explained to first-year students and is also beautiful, in my opinion.

2012-08-03 (3. August 2012)
Is the limit used in each entry the limsup?
2012-08-04 (4. August 2012)
Yes you can think of it either as the limsup or as a limit if you equip the disjoint union of the reals with infinity with the right topology (the one-point compactification will do).
2012-08-05 (5. August 2012)
Lagrange thm should say that any subgroup H of a finite group G of order n has an order that divides n. (not iff)
2012-08-06 (6. August 2012)
Ahrg! Thank you for the correction. I tend to memorize it wrong... it is an interesting question in which situations the converse of Lagrange holds.