Some Interesting Rings
Monday, July 30th, 2012 | Author: Konrad Voelkel
You probably know the integers  which can be defined as the Grothendieck group of the monoid of natural numbers
which can be defined as the Grothendieck group of the monoid of natural numbers  which exists by the axioms of Zermelo-Fraenkel set theory and probably in almost all other axiom systems as well. So the integers are a quite fundamental object in mathematics (did I really just argue for that? Well, now I did).
which exists by the axioms of Zermelo-Fraenkel set theory and probably in almost all other axiom systems as well. So the integers are a quite fundamental object in mathematics (did I really just argue for that? Well, now I did).
It is also natural to look what one can derive from the integers. In this short article I want to describe some rings that can be obtained from the integers by quotients, subgroups, products, and in general (co)limits and combinations thereof. The purpose might not be so clear, but it was a by-product of other investigations and I hope it could be interesting to say something about some concrete rings.
 is a torsion-free ring which has residue fields in any characteristics. It is a noetherian principal ideal domain. The abelian group
is a torsion-free ring which has residue fields in any characteristics. It is a noetherian principal ideal domain. The abelian group  generates the category of abelian groups, since every abelian group can be written by generators and relations and this corresponds to a surjection of some power of
generates the category of abelian groups, since every abelian group can be written by generators and relations and this corresponds to a surjection of some power of  onto the group (and the relations generate the kernel). Every abelian group is a
onto the group (and the relations generate the kernel). Every abelian group is a  -module just by the operation
-module just by the operation  (
( times).
times). is a finite (hence noetherian) torsion ring, and we have maps
is a finite (hence noetherian) torsion ring, and we have maps  given by reduction modulo
given by reduction modulo  . One can also write down (non-canonically) an isomorphism of groups
. One can also write down (non-canonically) an isomorphism of groups  , the group of
, the group of  -th roots of unity, by mapping a generator to a primitive
-th roots of unity, by mapping a generator to a primitive  -th root of unity. Under this isomorphism, the map "reduction mod
-th root of unity. Under this isomorphism, the map "reduction mod  " corresponds to taking the
" corresponds to taking the  -th power of a
-th power of a  -th root of unity to obtain a
-th root of unity to obtain a  -th root of unity.
-th root of unity. is a field of characteristics 0 with ring of integers
is a field of characteristics 0 with ring of integers  , i.e. it is the field of fractions of
, i.e. it is the field of fractions of  . As an abelian group,
. As an abelian group,  is divisible, so it is an injective object in the category of abelian groups.
is divisible, so it is an injective object in the category of abelian groups.  -modules are the same as
-modules are the same as  -vector spaces.
-vector spaces. is a ring in which every element is torsion, since
is a ring in which every element is torsion, since  , with
, with  many summands, equals
many summands, equals  , so is
, so is 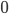 in
in  . As a quotient of a divisible group,
. As a quotient of a divisible group,  is divisible. It is a cogenerator of the category of abelian groups, i.e. every abelian group maps injectively in a sufficiently large power of
is divisible. It is a cogenerator of the category of abelian groups, i.e. every abelian group maps injectively in a sufficiently large power of  (this gives us the fact, that the category of abelian groups has enough injectives).
(this gives us the fact, that the category of abelian groups has enough injectives). is the completion of
is the completion of  at the prime
at the prime 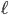 , i.e. at the
, i.e. at the 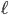 -adic valuation (hence has a nontrivial topology). One can also define equivalently
-adic valuation (hence has a nontrivial topology). One can also define equivalently  and the corresponding limit topology is the same as the completion topology. It contains
and the corresponding limit topology is the same as the completion topology. It contains  . It is also torsion-free of characteristics 0 and has residue field
. It is also torsion-free of characteristics 0 and has residue field  (did I mention that
(did I mention that 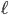 is prime?
is prime? 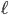 is always prime).
is always prime). is the field of fractions of
is the field of fractions of  , and one can also write
, and one can also write  .
. is the profinite completion of the integers
is the profinite completion of the integers  . It is torsion-free.
. It is torsion-free. , where the
, where the  means the restricted product, which is a subset of the product given by elements which have only finitely many entries not in
means the restricted product, which is a subset of the product given by elements which have only finitely many entries not in  . It has a natural topology making it a topological ring, which is different from the subspace topology. Oh, by the way, this ring is called the finite Adèles. The product
. It has a natural topology making it a topological ring, which is different from the subspace topology. Oh, by the way, this ring is called the finite Adèles. The product  is called the Adèles (of
is called the Adèles (of  ).
).![\mathbb{Z}[x_1,\dots]](http://www.konradvoelkel.com/wp-content/plugins/latex/cache/tex_41545197357eea5db9f1e400d6869ee7.gif) , a polynomial ring in countably infinite many variables, has every finitely generated ring as quotient ring. This generalizes to higher cardinalities. @Jan: thanks for this addition to the list.
, a polynomial ring in countably infinite many variables, has every finitely generated ring as quotient ring. This generalizes to higher cardinalities. @Jan: thanks for this addition to the list.
Do you know more interesting rings derived from these? Did I miss interesting properties?

2012-10-18 (18. October 2012)
Any ring is a quotient of a polynomial ring over $\mathbb Z$ in infinitely many variables.