Every simplicial set admits a universal covering space. If the simplicial set is a simplicial group, the covering can be given a group structure, such that the covering map is a group homomorphism. This can be done "at once" without using geometric realizations, just by close analysis of the usual construction of the universal covering.

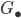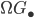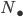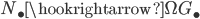Let $G_\bullet$ be a simplicial group, $PG_\bullet$ its path space, $\Omega G_\bullet$ its loop space and $N_\bullet$ the kernel of the projection $\Omega G_\bullet \rightarrow \pi_1(G_\bullet, id)$, which consists of all contractible loops. The composition of $N_\bullet \hookrightarrow \Omega G_\bullet$ with the inclusion 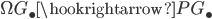$\Omega G_\bullet \hookrightarrow PG_\bullet$ yields a monomorphism 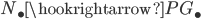$N_\bullet \hookrightarrow PG_\bullet$ whose cokernel we denote by $\tilde{G}_\bullet$.

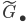I claim that this simplicial group already does the job.

To see this, we stare at the following commutative diagram

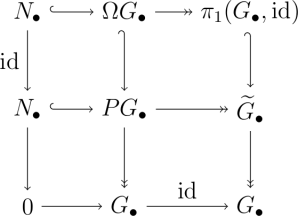
with exact rows by construction.
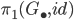The left hand column is trivially exact, the middle column is exact by definition of the loop space, and by a diagram chase (special case of the 9-lemma) we get exactness of the right hand column. So we have proved that the fibration $\tilde{G}_\bullet \rightarrow G_\bullet$ with discrete fiber has kernel $\pi_1(G_\bullet,id)$. The corresponding fiber sequence yields in the lower terms an exact sequence

$$0 \to \pi_1(\tilde{G}_\bullet,id) \to \pi_1(G_\bullet,id) \to \pi_1(G_\bullet,id) \to \pi_0(\tilde{G}_\bullet,id) \to 0$$

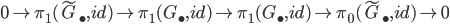
where the middle arrow $\pi_1(G_\bullet,id) \to \pi_1(G_\bullet,id)$ is an isomorphism, so we know that $\pi_1(\tilde{G}_\bullet,id)$ and $\pi_0(\tilde{G}_\bullet,id)$ are trivial.
From the same fiber sequence we obtain that for all $n \geq 2$ there is an isomorphism $\pi_n(\tilde{G}_\bullet,id) \simeq \pi_n(G_\bullet,id)$.

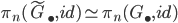I do not claim this proof to be new (it is way too simple), but I haven't found it in the literature and it might help understanding how the tools involved work, so this is expository work. For the notation and objects used, you can consider the book of Goerss and Jardine: Simplicial Homotopy Theory.

I do not like the proof via geometric realization, which roughly goes like that: Take a simplicial group, realize it to a topological group, construct the group structure on the fiber over the basepoint and on a neighbourhood around the basepoint, show that this is somehow compatible, take the singular resolution and see that this is a simplicial group covering something which is weakly equivalent to the original thing. I suspect most of my readers know how to prove that the universal covering of a Lie group is a Lie group again. The usual proof of this is similar to the argument done after geometric realization.

Someone remarked that the diagram above resembles the octahedral axiom. Can you make sense of this?