A¹-fundamental groups of isotropic groups
Friday, July 20th, 2012 | Author: Konrad Voelkel
Last week Matthias Wendt and I have put our first joint paper on the arXiv, it's called "A¹-fundamental groups of isotropic reductive groups" and here I will tell you how you can think about it without going through all definitions.
I have blogged about this before, but until a few days ago, there was only my diploma thesis in german and an extended abstract in english online, and the results were not as general (oh, and the proofs were also not the best...).
Isotropic what?
I have previously written an explanation of reductive groups to anyone who knows a little bit about algebraic groups.
If you stumble upon "isotropic reductive group", just think of  or
or  (as an algebraic group, defined over the integers). These are Chevalley groups of universal type, in particular they are split (the maximal torus is a
(as an algebraic group, defined over the integers). These are Chevalley groups of universal type, in particular they are split (the maximal torus is a  -split torus). A more general reductive group might be defined over some field
-split torus). A more general reductive group might be defined over some field  but the maximal torus splits only over an extension
but the maximal torus splits only over an extension  . This is what happens for
. This is what happens for  with D a central division algebra, or for
with D a central division algebra, or for 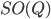 with Q a non-split quadratic form. The word "isotropic" refers to the maximal split torus, which should be of rank at least 2 (and yes, it is a slightly artificial definition, you would expect the rank to be at least 1, but right now one needs to have a 2 here).
with Q a non-split quadratic form. The word "isotropic" refers to the maximal split torus, which should be of rank at least 2 (and yes, it is a slightly artificial definition, you would expect the rank to be at least 1, but right now one needs to have a 2 here).
The theory of isotropic reductive groups and their elementary subgroups has been worked out by Tits, Weiss, Petrov, Stavrova, Luzgarev and others.
Motivic, A¹, WTF?
As a first approximation, think of A¹-fundamental groups as an analogue of classical fundamental groups of topological spaces, in the spirit of loops modulo homotopy. Don't confuse it with various notions of "algebraic" fundamental groups like Galois groups or étale fundamental groups which have no direct generalization to higher homotopy groups. The A¹-fundamental group is just one in a series of  , as in classical topology, and there is a good theory of fiber sequences and cofiber sequences.
, as in classical topology, and there is a good theory of fiber sequences and cofiber sequences.
Some classical topology at least, and more ...
Well, there is one notion of "algebraic" fundamental group of a group G that is somewhat similar, but differs in general, which is the second group cohomology of the trivial G-module  ,
,  . This group classifies central extensions of G, so in some sense it is analogous of the fundamental group, which classifies coverings. A central extension is just a group homomorphism such that the kernel lies in the center of the domain. If the group G is perfect (i.e. equals its own commutator subgroup), there is a universal central extension
. This group classifies central extensions of G, so in some sense it is analogous of the fundamental group, which classifies coverings. A central extension is just a group homomorphism such that the kernel lies in the center of the domain. If the group G is perfect (i.e. equals its own commutator subgroup), there is a universal central extension

and one can identify
 .
.
There is a world where the two notions can be compared, namely for topological groups. If you take a perfect connected topological group G, you can classify its central extensions by  and its coverings by
and its coverings by  (with natural basepoint the neutral element).
(with natural basepoint the neutral element).
Any covering of a topological group can be thought of as a group homomorphism, since the universal cover  carries a natural group structure (as I explained in the simplicial setting before). Now every such covering group homomorphism is central, so in some sense
carries a natural group structure (as I explained in the simplicial setting before). Now every such covering group homomorphism is central, so in some sense  is bigger than
is bigger than  and there is a morphism of central extensions from the universal central extension to the universal cover.
and there is a morphism of central extensions from the universal central extension to the universal cover.


I'm sorry that I don't explain the part of the story where  and
and  are compared, which is beautiful mathematics in its own right.
are compared, which is beautiful mathematics in its own right.
If you're into homotopy theory, you may want to replace topological groups with simplicial groups, since it is easier to work with simplicial objects sometimes. The comparison just sketched is still there, but now we can apply this setting to a particular example:
Take the algebraic group  (or
(or  ) and some infinite field
) and some infinite field  , then we can take
, then we can take  to be an ordinary group, and each
to be an ordinary group, and each ![SL_n(k[t_1,...,t_n])](http://www.konradvoelkel.com/wp-content/plugins/latex/cache/tex_2a272343d1153e923a6514f84362d04f.gif) will also be an ordinary group. One can define face and boundary maps that make
will also be an ordinary group. One can define face and boundary maps that make ![SL_n(k[t_1,...,t_\ast])](http://www.konradvoelkel.com/wp-content/plugins/latex/cache/tex_9135cd2f46ae16c5a1e54cb690dd2446.gif) into a simplicial object in the category of groups, denoted
into a simplicial object in the category of groups, denoted ![SL_n(k[\Delta^\bullet])](http://www.konradvoelkel.com/wp-content/plugins/latex/cache/tex_4bec5e63c61b5bbdb51e7458c7c62415.gif) , since the variables
, since the variables  are thought of as the coordinates of an n-simplex. Another common notation is
are thought of as the coordinates of an n-simplex. Another common notation is  , which has the conceptual difference that one considers
, which has the conceptual difference that one considers 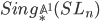 as a functor from rings to simplicial groups, and
as a functor from rings to simplicial groups, and  as a functor from algebraic varieties to functors from rings to simplicial sets. This functor
as a functor from algebraic varieties to functors from rings to simplicial sets. This functor  is called singular replacement (or Suslin-Voevodsky construction).
is called singular replacement (or Suslin-Voevodsky construction).
Altogether, we can now compute the simplicial fundamental group of the  -points of the singular replacement
-points of the singular replacement  , and the nice thing happening is that it's isomorphic to
, and the nice thing happening is that it's isomorphic to  . It is also known that this homology group is presentable (by H. Matsumoto), the presentation is commonly known as second Milnor K-theory
. It is also known that this homology group is presentable (by H. Matsumoto), the presentation is commonly known as second Milnor K-theory 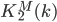 and depends only on the field
and depends only on the field  . By abstract blabla, one also identifies
. By abstract blabla, one also identifies  with the second Quillen K-Theory
with the second Quillen K-Theory  .
.
Small warning: For  instead of
instead of  the picture is slightly skewed, since
the picture is slightly skewed, since  is no longer isomorphic to Quillen K-Theory, but the corresponding symplectic version, and the presentation doesn't yield Milnor K-Theory, but some symplectic version, which can be shown to be isomorphic to the so-called Milnor-Witt K-Theory of Morel & Hopkins.
is no longer isomorphic to Quillen K-Theory, but the corresponding symplectic version, and the presentation doesn't yield Milnor K-Theory, but some symplectic version, which can be shown to be isomorphic to the so-called Milnor-Witt K-Theory of Morel & Hopkins.
Bigger warning: For non-split groups, there is no presentation by Matsumoto any longer. The only case known so far is  , by a theorem of Rehmann.
, by a theorem of Rehmann.
Let's make a polynomial fundamental group!
There are two explanations what is happening here, a simple and an interesting one. Of course we start with the simple one:
If you take  , with
, with  a topological field, you can look at all coverings, classified by
a topological field, you can look at all coverings, classified by  , a group defined by continuous loops modulo continuous homotopies. It is a very natural question to ask: What happens if we restrict ourselves to polynomial loops (maps from
, a group defined by continuous loops modulo continuous homotopies. It is a very natural question to ask: What happens if we restrict ourselves to polynomial loops (maps from  to
to  that have the same values at 0 and 1) modulo polynomial homotopies (maps from
that have the same values at 0 and 1) modulo polynomial homotopies (maps from  to
to  )?
)?
On one hand, we would expect the resulting group to be smaller, since there are fewer loops. On the other hand, there are also fewer homotopies, so there are not as many relations as in the continuous case.
We can make the question very precise, by asking what the fundamental group of  looks like (it really boils down to that). From what I sketched above, we get the answer: the polynomial loops modulo polynomial homotopies (that are defined over
looks like (it really boils down to that). From what I sketched above, we get the answer: the polynomial loops modulo polynomial homotopies (that are defined over  ) classify the central extensions of
) classify the central extensions of  . Beautiful, isn't it?
. Beautiful, isn't it?
This works for any isotropic reductive group instead of  , but in the split case, where Matsumoto's theorem is available, we can explicitly describe the generating loops that come from symbols in Milnor- or Milnor-Witt K-Theory (one can write down matrices in polynomials in one variable).
, but in the split case, where Matsumoto's theorem is available, we can explicitly describe the generating loops that come from symbols in Milnor- or Milnor-Witt K-Theory (one can write down matrices in polynomials in one variable).
A crucial ingredient for this to work is homotopy invariance (in one variable) of group homology, as shown by Wendt.
A¹-homotopy-theoretical side
Now for the more interesting explanation: The simplicial group object 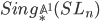 in the category of functors from rings to sets can be thought of as presheaf on the category of smooth schemes over
in the category of functors from rings to sets can be thought of as presheaf on the category of smooth schemes over  . There is a formalism (worked out by Morel and Wendt) that allows to identify its values over rings like
. There is a formalism (worked out by Morel and Wendt) that allows to identify its values over rings like  with the sections over
with the sections over  of the
of the  -fundamental group
-fundamental group  . This formalism is called the affine Brown-Gersten property and I'll explain how it works now.
. This formalism is called the affine Brown-Gersten property and I'll explain how it works now.
Suppose you have a presheaf F, then you can ask whether it is a sheaf, usually characterized by a diagram required to be a coequalizer if one works with pretopologies. The Zariski, Nisnevich and étale topology allow a nice characterization by elementary cartesian squares, which are essentially coverings by just two arrows. The sheaf property is then expressed as: all elementary squares are mapped by F to cocartesian squares. We can define the notion of a homotopy sheaf by requiring F to map the elementary squares only to homotopy-cocartesian squares. If F is a homotopy sheaf, one also says that F has the Brown-Gersten property (all with respect to the particular topology, of course). If one requires F to "respect" only those elementary cartesian squares which consist of affine schemes, then F has the affine Brown-Gersten property.
Abstract homotopy works like that: If you want to define the homotopy groups of some object X in a model category, you first take a fibrant replacement, and then you can write down more explicitly what it should be. In the model category of simplicial sets, one is lucky that Moore's Lemma tells us that simplicial groups are already fibrant, so we can compute the fundamental group really by certain 1-simplices (loops) modulo certain 2-simplices (homotopies). In the model category of topological spaces, it's even cheaper, since all objects are fibrant, and one can write down every fundamental group as loops modulo homotopies.
In the A¹-model category of Morel and Voevodsky, the objects are simplicial sheaves in the Nisnevich topology, and the fibrant replacement is very hard to control, so it is very very hard to compute any homotopy groups. That's where the singular replacement is handy: in some situations, the simplicial fundamental group of the sections of the singular replacement over an affine scheme A,  is isomorphic to the sections of the A¹-fundamental group of F over A,
is isomorphic to the sections of the A¹-fundamental group of F over A,  . One situation where one has such an isomorphism is when F has the affine Brown-Gersten property and also A¹-invariance.
. One situation where one has such an isomorphism is when F has the affine Brown-Gersten property and also A¹-invariance.
One can define an "affine replacement" of F, and if F has the affine Brown-Gersten property and A¹-invariance, this affine replacement has the Brown-Gersten property. Altogether, one can then see that the simplicial homotopy groups of sections over affines are isomorphic to the sections over affines of the A¹-homotopy groups.
Matthias Wendt proved that Chevalley groups of universal type have the affine Brown-Gersten property in the Nisnevich topology in the paper "A¹-homotopy of Chevalley groups" which is now generalized to isotropic reductive groups in this paper, so in that sense it's a sequel.
I would like to mention more of what's in the paper, but then I would probably just write it up again, far less structured than it is on the arXiv now, so I stop here.
