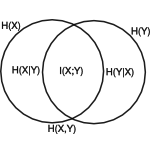
Questions in Information Theory III: Statistical Physics, Quantum Physics and Thermodynamics
Thursday, October 28th, 2010 | Author: Konrad Voelkel
See also: Questions part I - Information and Entropy
Questions part II - Complexity and Algorithmic Complexity
Questions part III - Statistical Physics, Quantum Physics and Thermodynamics [GM94] [Pen05]
- Can there be some kind of Maxwell’s daemon, and why (not)?
- Can all analog information be transformed to digital information losslessly?
Is physical information always digital (digital philosophy)? - Does the second law of thermodynamics depend on a human observer?
- Can quantum mechanical entanglement be reduced to mutual information? [NC00] [DH00] [PV06] [BP07]
- What is the mathematical, what is the physical content of Heisenberg’s uncertainty relation?
“I think I can safely say that nobody understands quantum mechanics.” – Richard Phillips Feynman, 1965
- Is there a method to denote and calculate, for an open physical system, how the information content changes in time when the system’s dynamics are known?
- Is there an important difference between information loss into small scales and information loss into microscopic freedoms?
- Where do (thermal, quantum, vacuum, ?) fluctuations come from? [Lam97] [Lam98]
What do they change on the macroscopic scale?
Are gravitational fluctuations possible? - According to Einstein’s fluctuation-dissipation-theorem, do thermal fluctuations compensate exactly for information loss through dissipation? [CW51]
- Is probability theory powerful enough to capture any micro-physical phenomena?
Is mathematical probability theory the correct language for modern physics? [Mil04]“In fact the smallest units of matter are not physical objects in the ordinary sense; they are forms, ideas which can be expressed unambiguously only in mathematical language.” – Werner Heisenberg, 1992
- How is Zeilinger’s concept of elementary systems generalizable to general state spaces?
- Given the fact that every system is continually measured, is the concept of a closed quantum system (with unitary time evolution) relevant for real physics? [And97]
Does decoherence by interference with the background universe render the concept of closed quantum systems obsolete? [BTV09] - How does randomness in quantum measurement emerge from unitary evolution?
Is quantum physics truly information-preserving? - How relevant is the classical concept of degree of freedom for quantum mechanics?
References
- [And97] Philip W. Anderson, Is measurement itself an emergent property?, Complex. 3 (1997), no. 1, 14–16.
- [BP07] S.L. Braunstein and A.K. Pati, Quantum information cannot be completely hidden in correlations: Implications for the black-hole information paradox, Physical Review Letters 98 (2007).
- [BTV09] Buchleitner, Tiersch, and Viviescas, Entanglement and decoherence, Lecture Notes in Physics, Springer, 2009.
- [CW51] Herbert B. Callen and Theodore A. Welton, Irreversibility and generalized noise, Phys. Rev. 83 (1951), no. 1, 34–40.
- [DH00] D. Deutsch and P. Hayden, Information flow in entangled quantum systems, Proceedings: Mathematics, Physical and Engineering Sciences 456 (2000), no. 1999, 1759–1774.
- [GM94] M. Gell-Mann, The quark and the jaguar, Freeman New York, 1994.
- [Lam97] SK Lamoreaux, Demonstration of the casimir force in the 0.6 to 6 µm range, Physical Review Letters 78 (1997), no. 1, 5–8.
- [Lam98] S. K. Lamoreaux, Erratum: Demonstration of the casimir force in the 0.6 to 6 µm range [phys. rev. lett. 78, 5 (1997)], Phys. Rev. Lett. 81 (1998), no. 24, 5475–5476.
- [Mil04] David Miller, Probability generalizes logic, 2004.
- [NC00] Nielsen and Chuang, Quantum computation and quantum information, 2000.
- [Pen05] Roger Penrose, The road to reality: A complete guide to the laws of the universe, 3 ed., Knopf, 2005.
- [PV06] Martin B. Plenio and S. Virmani, An introduction to entanglement measures, arXiv, Jun 2006.